题目内容
12.函数$y=\frac{cos6x}{{{2^x}-{2^{-x}}}}$的图象大致是( )| A. | 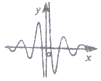 | B. | 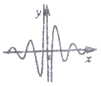 | C. |  | D. |  |
分析 判断函数的奇偶性,并计算特殊值即可得出答案.
解答 解:令f(x)=$\frac{cos6x}{{2}^{x}-{2}^{-x}}$,则f(-x)=$\frac{cos6x}{{2}^{-x}-{2}^{x}}$=-f(x),
∴f(x)是奇函数,图象关于原点对称,排除C,D;
令f(x)=0得cos6x=0,∴6x=$\frac{π}{2}$+kπ,x=$\frac{π}{12}$+$\frac{kπ}{6}$,k∈Z,
∴f(x)的最小正零点为$\frac{π}{12}$,
当x∈(0,$\frac{π}{12}$)时,2x>1>2-x,cos6x>0,∴f(x)>0,排除B,
故选A.
点评 本题考查了函数奇偶性的判断,函数值的计算,余弦函数的性质,属于中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
20.(1-2x)3的展开式中所有的二项式系数和为a,函数y=mx-2+1(m>0且m≠1)经过的定点的纵坐标为b,则${({bx+3y})^3}•{({x+\frac{5}{4}y})^5}$的展开式中x6y2的系数为( )
| A. | 320 | B. | 446 | C. | 482 | D. | 248 |
17.若实数变量x、y满足约束条件|x+y|+|x-2y|≤3,目标函数z=ax-y+1(a∈R).有如下结论:①可行域外轮廓为矩形;②可行域面积为3;③a=1时,z的最小值为-1;④a=2时,使得z取最大值的最优解有无数组;则下列组合中全部正确的为( )
| A. | ①② | B. | ②③ | C. | ①③ | D. | ③④ |
1.如图1为某市2017年2月28天的日空气质量指数折线图.
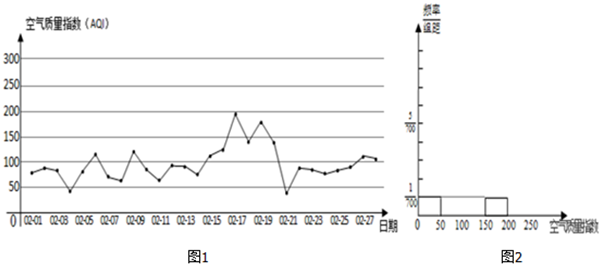
由中国空气质量在线监测分析平台提供的空气质量指数标准如下:
(Ⅰ)请根据所给的折线图补全如图2所示的频率分布直方图(并用铅笔涂黑矩形区域),并估算该市2月份空气质量指数监测数据的平均数(保留小数点后一位);
(Ⅱ)在该月份中任取两天,求空气质量至少有一天为优或良的概率;
(Ⅲ)如果该市对环境进行治理,治理后经统计,每天的空气质量指数近似满足X~N(75,552),则治理后的空气质量指数均值大约下降了多少?

由中国空气质量在线监测分析平台提供的空气质量指数标准如下:
| 空气质量指数 | (0,50] | (50,100] | (100,150] | (150,200] | (200,300] | 300以上 |
| 空气质量等级 | 1级优 | 2级良 | 3级轻度污染 | 4级中度污染 | 5级重度污染 | 6级严重污染 |
(Ⅱ)在该月份中任取两天,求空气质量至少有一天为优或良的概率;
(Ⅲ)如果该市对环境进行治理,治理后经统计,每天的空气质量指数近似满足X~N(75,552),则治理后的空气质量指数均值大约下降了多少?
2.某校高三共有900名学生,高三模拟考之后,为了了解学生学习情况,用分层抽样方法从中抽出若干学生此次数学成绩,按成绩分组,制成如下的频率分布表:
(1)若频数的总和为c,试求a,b,c的值;
(2)为了了解数学成绩在120分以上的学生的心理状态,现决定在第六、七、八组中用分层抽样方法抽取6名学生,在这6名学生中又再随机抽取2名与心理老师面谈,令第七组被抽中的学生数为随机变量ξ,求随机变量ξ的分布列和数学期望;
(3)估计该校本次考试的数学平均分.
| 组号 | 第一组 | 第二组 | 第二组 | 第四组 |
| 分组 | [70,80) | [80,90) | [90,100) | [100,110) |
| 频数 | 6 | 4 | 22 | 20 |
| 频率 | 0.06 | 0.04 | 0.22 | 0.20 |
| 组号 | 第五组 | 第六组 | 第七组 | 第八组 |
| 分组 | [110,120) | [120,130) | [130,140) | [140,150] |
| 频数 | 18 | a | 10 | 5 |
| 频率 | b | 0.15 | 0.10 | 0.05 |
(2)为了了解数学成绩在120分以上的学生的心理状态,现决定在第六、七、八组中用分层抽样方法抽取6名学生,在这6名学生中又再随机抽取2名与心理老师面谈,令第七组被抽中的学生数为随机变量ξ,求随机变量ξ的分布列和数学期望;
(3)估计该校本次考试的数学平均分.



