题目内容
设数列{an}的前n项和为Sn=2n2,{bn}为等比数列,且a1=b1,b2(a2-a1)=b1.
(1)求数列{an}和{bn}的通项公式;( 6分)
(2)设cn=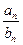 ,求数列{cn}的前n项和Tn.
,求数列{cn}的前n项和Tn.
(1)求数列{an}和{bn}的通项公式;( 6分)
(2)设cn=
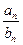 ,求数列{cn}的前n项和Tn.
,求数列{cn}的前n项和Tn.22. (1) 当n=1时,a1=S1=2
当n≥2时,an=Sn-Sn-1=2n2-2(n-1)2=4n-2,
又a1=2满足上式,
∴an=4n-2. ………………………………………3分
设{bn}的公比为q,由b2(a2-a1)=b1知,b1=2,b2= ,所以q=
,所以q= ,
,
∴bn=b1qn-1=2× ,即bn=
,即bn= . …………………………6分
. …………………………6分
(2)∵cn=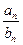 =
= =(2n-1) 4n-1, …………………………8分
=(2n-1) 4n-1, …………………………8分
∴Tn=1+3×41+5×42+…+(2n-1)4n-1 ①
又4Tn=1×41+3×42+5×42+…+(2n-3)4n-1+(2n-1)4n ②……………10分
①-②得:-3Tn= 1+2(41+42+43+…+4n-1)-(2n-1)4n
= -(2n-1)4n
-(2n-1)4n
=
∴Tn= [(6n-5)4n+5].
[(6n-5)4n+5].
当n≥2时,an=Sn-Sn-1=2n2-2(n-1)2=4n-2,
又a1=2满足上式,
∴an=4n-2. ………………………………………3分
设{bn}的公比为q,由b2(a2-a1)=b1知,b1=2,b2=
 ,所以q=
,所以q= ,
,∴bn=b1qn-1=2×
 ,即bn=
,即bn= . …………………………6分
. …………………………6分(2)∵cn=
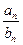 =
= =(2n-1) 4n-1, …………………………8分
=(2n-1) 4n-1, …………………………8分∴Tn=1+3×41+5×42+…+(2n-1)4n-1 ①
又4Tn=1×41+3×42+5×42+…+(2n-3)4n-1+(2n-1)4n ②……………10分
①-②得:-3Tn= 1+2(41+42+43+…+4n-1)-(2n-1)4n
=
 -(2n-1)4n
-(2n-1)4n=

∴Tn=
 [(6n-5)4n+5].
[(6n-5)4n+5].略

练习册系列答案
 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案
相关题目
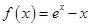 (
(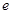 是自然对数的底数)
是自然对数的底数)
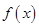 的最小值;
的最小值;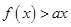 的解集为P, 若
的解集为P, 若
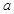 的取值范围;
的取值范围;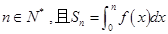 ,是否存在等差数列
,是否存在等差数列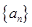 和首项为
和首项为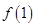 公比大于0的等比数列
公比大于0的等比数列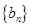 ,使数列
,使数列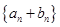 的前n项和等于
的前n项和等于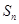
 +
+ +
+ +…
+…
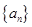 的前n项和
的前n项和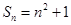 ,则
,则 =
=
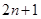


 的前
的前 项和
项和 ,对于任意的
,对于任意的 ,都满足
,都满足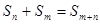 ,
,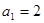 ,则
,则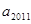 等于( )
等于( )
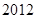

 的前n项和为
的前n项和为 ,
, 且
且 ,则n=( )
,则n=( ) 对任意的正整数n,都有
对任意的正整数n,都有 (d为常数),则称
(d为常数),则称 ,“绝对公和”
,“绝对公和” ,则其前2010项和
,则其前2010项和 的最小值为
的最小值为  ,则
,则 等于( )
等于( ) 



 中,
中, 前
前 项和为
项和为 ,且点
,且点 在直线
在直线 上,则
上,则 =( )
=( )


