题目内容
(本小题满分14分)已知函数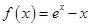 (
(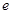 是自然对数的底数)
是自然对数的底数)

(1)求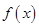 的最小值;
的最小值;
(2)不等式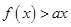 的解集为P, 若
的解集为P, 若
求实数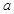 的取值范围;
的取值范围;
(3)已知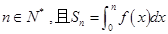 ,是否存在等差数列
,是否存在等差数列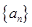 和首项为
和首项为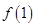 公比大于0的等比数列
公比大于0的等比数列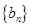 ,使数列
,使数列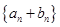 的前n项和等于
的前n项和等于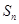
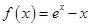 (
(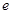 是自然对数的底数)
是自然对数的底数)
(1)求
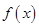 的最小值;
的最小值;(2)不等式
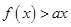 的解集为P, 若
的解集为P, 若
求实数
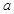 的取值范围;
的取值范围;(3)已知
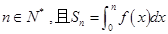 ,是否存在等差数列
,是否存在等差数列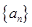 和首项为
和首项为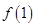 公比大于0的等比数列
公比大于0的等比数列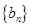 ,使数列
,使数列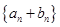 的前n项和等于
的前n项和等于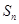
解:(Ⅰ)
当 时,
时, ; 当
; 当 时,
时,
故 连续,故
连续,故 ————3分
————3分
(Ⅱ) 即不等式
即不等式 在区间
在区间 有解
有解 可化为
可化为 ,
, 在区间
在区间 有解————4分
有解————4分
令 ————5分
————5分
 故
故 在区间
在区间 递减,在区间
递减,在区间 递增
递增

所以,实数a的取值范围为 —————8分
—————8分
(Ⅲ)设存在公差为d首项等于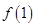 的等差数列
的等差数列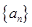
和公比q大于0的等比数列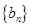 ,使得数列
,使得数列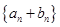 的前n项和等于
的前n项和等于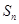

故
即 ①,
①,  ②
②
②-①×2得 ,
,  (舍去)
(舍去)
故 ,
, ,此时,
,此时, 数列
数列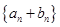 的的前n项和等于
的的前n项和等于

故存在满足题意的等差数列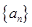 金额等比数列
金额等比数列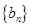 ,
,
使得数列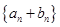 的前n项和等于
的前n项和等于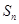 ————14分
————14分

当
 时,
时, ; 当
; 当 时,
时,
故
 连续,故
连续,故 ————3分
————3分(Ⅱ)
 即不等式
即不等式 在区间
在区间 有解
有解 可化为
可化为 ,
, 在区间
在区间 有解————4分
有解————4分令
 ————5分
————5分 故
故 在区间
在区间 递减,在区间
递减,在区间 递增
递增
所以,实数a的取值范围为
 —————8分
—————8分(Ⅲ)设存在公差为d首项等于
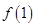 的等差数列
的等差数列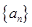
和公比q大于0的等比数列
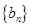 ,使得数列
,使得数列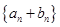 的前n项和等于
的前n项和等于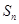

故

即
 ①,
①,  ②
②②-①×2得
 ,
,  (舍去)
(舍去)故
 ,
, ,此时,
,此时, 数列
数列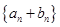 的的前n项和等于
的的前n项和等于
故存在满足题意的等差数列
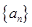 金额等比数列
金额等比数列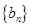 ,
,使得数列
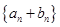 的前n项和等于
的前n项和等于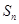 ————14分
————14分略

练习册系列答案
相关题目
 的定义域为R,数列
的定义域为R,数列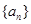 满足
满足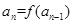 (
(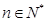 且
且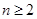 ).
).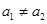 ,且
,且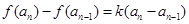 (k为非零常数,
(k为非零常数, 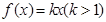 ,
,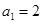 ,
,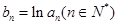 ,数列
,数列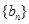 的前n项和为
的前n项和为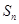 ,对于给定的正整数
,对于给定的正整数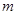 ,如果
,如果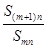 的值与n无关,求k的值.
的值与n无关,求k的值. 满足
满足
 ,若
,若 ,则
,则 的值为
的值为



 ,
, ,
,
 ,求数列
,求数列 的前
的前 项和
项和 }(
}( ∈N*)满足
∈N*)满足 ,
, 是其前n项的和,且
是其前n项的和,且 <
< ,
, ,则下列结论错误的是
,则下列结论错误的是 <0
<0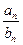 ,求数列{cn}的前n项和Tn.
,求数列{cn}的前n项和Tn.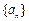 满足:
满足: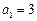 ,
,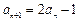 ,
,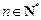 .计算得
.计算得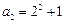 ,
,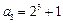 .
.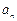 ,并用数学归纳法加以证明;
,并用数学归纳法加以证明; 满足
满足 ,若
,若 ,则
,则




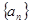 的前
的前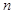 项和为
项和为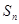 ,点
,点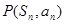 在直线
在直线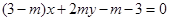 上,(
上,(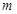 为常数,
为常数,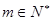 ,
,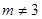 ).
).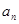 ;
;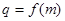 ,数列
,数列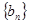 满足
满足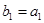 ,
,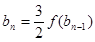 ,
,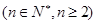 ,求证:
,求证: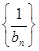 为等差
为等差 数列,并求
数列,并求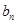 ;
;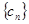 满足
满足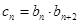 ,
,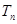 为数列
为数列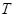 满足
满足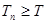
 ,求
,求