��Ŀ����
��X��һ���ǿռ��ϣ�����X�����ɸ��Ӽ���ɵļ��ϣ������㣺��∅�ʦӣ�X�ʦӣ��ڦ���������Ԫ�صIJ������ڦӣ��ۦ���������Ԫ�صĽ������ڦӣ���Ʀ���X�����ˣ���X={a��b��c}��������������ļ��Ϧӣ�
��1����={∅��{a}��{b}��{a��c}��{a��b��c}}��
��2����={∅��{a}��{c}��{a��c}��{a��b��c}}��
��3����={∅��{a}��{a��b}��{a��c}��{a��b��c}}��
��4����={∅��{a}��{a��b}��{b��c}��{a��b��c}}
����Ǽ���X�����˵ĸ����ǣ�������
��1����={∅��{a}��{b}��{a��c}��{a��b��c}}��
��2����={∅��{a}��{c}��{a��c}��{a��b��c}}��
��3����={∅��{a}��{a��b}��{a��c}��{a��b��c}}��
��4����={∅��{a}��{a��b}��{b��c}��{a��b��c}}
����Ǽ���X�����˵ĸ����ǣ�������
| A��1 | B��2 | C��3 | D��4 |
���㣺���мĺ�������
ר�⣺����
�������������˵Ķ��壬���Ԫ�غͼ��ϵĹ�ϵ���ɵõ����ۣ�
���
�⣺��1������={∅��{a}��{b}��{a��c}��{a��b��c}}ʱ��{a}��{b}={a��b}∉�ӣ��ʣ�1�����Ǽ���X�ϵ����˵ļ��Ϧӣ�
��2������={∅��{a}��{c}��{a��c}��{a��b��c}}ʱ�����㣺��X���ڦӣ�∅���ڦӣ��ڦ���������Ԫ�صIJ������ڦӣ��ۦ���������Ԫ�صĽ������ڦӣ���ˣ�2���Ǽ���X�ϵ����˵ļ��Ϧӣ�
��3������={∅��{a}��{a��b}��{a��c}��{a��b��c}}ʱ�����㣺��X���ڦӣ�∅���ڦӣ��ڦ���������Ԫ�صIJ������ڦӣ��ۦ���������Ԫ�صĽ������ڦӣ���ˣ�3���Ǽ���X�ϵ����˵ļ��Ϧӣ�
��4������={∅��{a}��{a��b}��{b��c}��{a��b��c}}ʱ�����㣺��X���ڦӣ�∅���ڦӣ��ڦ���������Ԫ�صIJ������ڦӣ��ۦ���������Ԫ�صĽ������ڦӣ���ˣ�4���Ǽ���X�ϵ����˵ļ��Ϧӣ�
�ʦ��Ǽ���X�����˵ĸ�����3����
��ѡ��C
��2������={∅��{a}��{c}��{a��c}��{a��b��c}}ʱ�����㣺��X���ڦӣ�∅���ڦӣ��ڦ���������Ԫ�صIJ������ڦӣ��ۦ���������Ԫ�صĽ������ڦӣ���ˣ�2���Ǽ���X�ϵ����˵ļ��Ϧӣ�
��3������={∅��{a}��{a��b}��{a��c}��{a��b��c}}ʱ�����㣺��X���ڦӣ�∅���ڦӣ��ڦ���������Ԫ�صIJ������ڦӣ��ۦ���������Ԫ�صĽ������ڦӣ���ˣ�3���Ǽ���X�ϵ����˵ļ��Ϧӣ�
��4������={∅��{a}��{a��b}��{b��c}��{a��b��c}}ʱ�����㣺��X���ڦӣ�∅���ڦӣ��ڦ���������Ԫ�صIJ������ڦӣ��ۦ���������Ԫ�صĽ������ڦӣ���ˣ�4���Ǽ���X�ϵ����˵ļ��Ϧӣ�
�ʦ��Ǽ���X�����˵ĸ�����3����
��ѡ��C
������������Ҫ����Ԫ�غͼ��Ϲ�ϵ���жϣ���ȷ�������˵Ķ����ǽ������Ĺؼ���

��ϰ��ϵ�д�
�����Ŀ
��������
����Ϊ��������Ϊ��ͨ�����ǣ�������
|
| A����x-1��2+��y+3��2=1 |
| B����x+3��2+��y-1��2=4 |
| C����x-2��2+��y+2��2=4 |
| D��x+y-2=0 |
 ��Сʱ�����Ǿ�����ָ��ϰ��������һ��С���Ѱ���ͼ��ʾ�Ĺ�����ϰ����������2014ʱ��Ӧ��ָͷ�ǣ�������
��Сʱ�����Ǿ�����ָ��ϰ��������һ��С���Ѱ���ͼ��ʾ�Ĺ�����ϰ����������2014ʱ��Ӧ��ָͷ�ǣ�������| A����Ĵָ | B��ʳָ |
| C����ָ | D������ָ |
��֪����{an}������m��n��N+����am+n=am+an+3����a1=3��������{an}��ͨ�ʽan=��������
| A��6n-3 | B��4n-1 |
| C��2n+1 | D��3n |
ƽ������n��Բ������ÿ����Բ���ཻ�����㣬��ÿ����Բ�������㣬��f��n����ʾ��n��Բ��ƽ��ָ������������ôf��n+1����f��n��֮��Ĺ�ϵΪ��������
| A��f��n+1��=f��n��+n |
| B��f��n+1��=f��n��+2n |
| C��f��n+1��=f��n��+n+1 |
| D��f��n+1��=f��n��+n-1 |
����������ABC�У���֪a2=b2+c2+bc�����AΪ��������
| A��60�� | B��120�� |
| C��30�� | D��60���120�� |
��֪��ԲO��
+
=1��������Ϊe1������ABC�����ڽ������Σ���
=
+
����AB���е�ΪD��D�Ĺ켣E��������Ϊe2��������
| x2 |
| a2 |
| y2 |
| b2 |
| OC |
| 3 |
| 5 |
| OA |
| 4 |
| 5 |
| OB |
| A��e1=e2 |
| B��e1��e2 |
| C��e1��e2 |
| D��e1e2=1 |
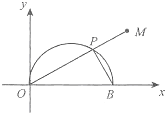 ��ֱ������xoy�У���OΪ���㣬x��������Ϊ���Ὠ��������ϵ������C�ļ����귽��Ϊ��=2cos�ȣ���ͼ������C��x�ύ��O��B���㣬P������C��x���Ϸ�ͼ��������һ�㣬����OP���ӳ���M��ʹPM=PB����P�仯ʱ����M�Ĺ켣�ij��ȣ�
��ֱ������xoy�У���OΪ���㣬x��������Ϊ���Ὠ��������ϵ������C�ļ����귽��Ϊ��=2cos�ȣ���ͼ������C��x�ύ��O��B���㣬P������C��x���Ϸ�ͼ��������һ�㣬����OP���ӳ���M��ʹPM=PB����P�仯ʱ����M�Ĺ켣�ij��ȣ�