Question

已知函数f（x）=

log2(1-x)+1，-1≤x＜0 x3-3x+2，0≤x≤a

的值域是[0，2]，则实数a的取值范围是（　　）

• A、（0，1]
• B、[1，

  3

  ]
• C、[1，2]
• D、[

  3

  ，2]

Answer 1

考点：分段函数的应用

专题：计算题,数形结合,函数的性质及应用

分析：先求出-1≤x＜0时，f（x）的范围（1，2]，再由题意得，[0，1]⊆{y|y=x³-3x+2，0≤x≤a}⊆[0，2]．画出函数y=x³-3x+2（0≤x≤a）的图象，令y=2，结合图象，即可得到a的取值范围．

解答： 解：∵函数f（x）=

log2(1-x)+1，-1≤x＜0 x3-3x+2，0≤x≤a

，
∴-1≤x＜0时，f（x）为减函数，1＜f（x）≤2，
∵函数f（x）的值域是[0，2]，
∴[0，1]⊆{y|y=x³-3x+2，0≤x≤a}⊆[0，2]．
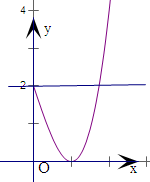
画出函数y=x³-3x+2（0≤x≤a）的图象，
y′=3x²-3，在0≤x≤1，y′≤0，x＞1时，y′＞0，
即[0，1]是减区间，y∈[0，2]，（1，+∞）为增区间，
且当y=2时，x³-3x=0，x=

3

（0，-

3

舍去），
∴由图象可知a的取值范围是[1，

3

]．
故选：B．

点评：本题考查分段函数及运用，考查函数的单调性及应用，考查数形结合的数学思想，是一道中档题．