题目内容
17. 已知椭圆E:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率e=$\frac{\sqrt{3}}{2}$,且过点($\frac{\sqrt{3}}{2}$,$\frac{1}{4}$).
已知椭圆E:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率e=$\frac{\sqrt{3}}{2}$,且过点($\frac{\sqrt{3}}{2}$,$\frac{1}{4}$).(Ⅰ)求椭圆E的方程;
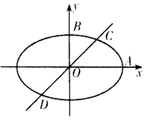
(Ⅱ)已知A、B分别为椭圆E的右顶点、上顶点,过原点O做斜率为k(k>0)的直线交椭圆于C、D两点,求四边形ACBD面积S的最大值.
分析 (Ⅰ)由题意列出关于a,b,c的方程组,求解方程组得到a,b的值,则椭圆方程可求;
(Ⅱ)由题意可设CD:y=kx,设C(x1,y1),D(x2,y2),到AB的距离分别为d1,d2,将y=kx代入椭圆方程可得x1,x2,进一步求出d1,d2,则四边形ACBD的面积S取得最大值可求.
解答 解:(Ⅰ)由题意可得:$\left\{\begin{array}{l}{\frac{c}{a}=\frac{\sqrt{3}}{2}}\\{\frac{3}{4{a}^{2}}+\frac{1}{16{b}^{2}}=1}\\{{a}^{2}={b}^{2}+{c}^{2}}\end{array}\right.$,解得a2=4,b2=1.
∴椭圆E的方程为$\frac{{x}^{2}}{4}+{y}^{2}=1$;
(Ⅱ)由题意可设CD:y=kx,设C(x1,y1),D(x2,y2),到AB的距离分别为d1,d2,
将y=kx代入$\frac{{x}^{2}}{4}+{y}^{2}=1$,得x2=$\frac{4}{1+4{k}^{2}}$,则x1=$\frac{2}{\sqrt{1+4{k}^{2}}}$,x2=-$\frac{2}{\sqrt{1+4{k}^{2}}}$.
由A(2,0),B(0,1)得|AB|=$\sqrt{5}$,且AB:x+2y-2=0,
d1=$\frac{{x}_{1}+2{y}_{1}-2}{\sqrt{5}}$,d2=-$\frac{{x}_{2}-2{y}_{2}-2}{\sqrt{5}}$,
S=$\frac{1}{2}$|AB|(d1+d2)=$\frac{1}{2}$[(x1-x2)+2(y1-y2)]
=$\frac{1}{2}$(1+2k)(x1-x2)=$\frac{2+4k}{\sqrt{1+4{k}^{2}}}$,
S2=4(1+$\frac{4k}{1+4{k}^{2}}$),
∵1+4k2≥4k,当且仅当4k2=1时取等号,
∴当k=$\frac{1}{2}$时,四边形ACBD的面积S取得最大值2$\sqrt{2}$.
点评 本题考查直线与圆的位置关系,考查了点到直线的距离公式的应用,考查计算能力,是中档题.

 名校课堂系列答案
名校课堂系列答案| A. | 54 | B. | 72 | C. | 78 | D. | 96 |
| A. | 相交 | B. | 内切 | C. | 外切 | D. | 内含 |
| A. | 充分而不必要条件 | B. | 必要而不充分条件 | ||
| C. | 充分必要条件 | D. | 既不充分也不必要条件 |
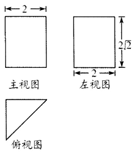 《九章算术》中将底面是直角三角形的直三棱柱称之为“堑堵”,已知某“堑堵”的三视图如图所示,则该“堑堵”的外接球的表面积为16π.
《九章算术》中将底面是直角三角形的直三棱柱称之为“堑堵”,已知某“堑堵”的三视图如图所示,则该“堑堵”的外接球的表面积为16π.