题目内容
6.已知函数$f(x)=\sqrt{-3{x^2}+ax}-\frac{a}{x}$(a>0).若存在x0,使得f(x0)≥0成立,则a的最小值为12$\sqrt{3}$.分析 若存在x0,使得f(x0)≥0成立,则函数$f(x)=\sqrt{-3{x^2}+ax}-\frac{a}{x}$(a>0)的最大值大于等于0,进而求得答案.
解答 解:若存在x0,使得f(x0)≥0成立,
则函数$f(x)=\sqrt{-3{x^2}+ax}-\frac{a}{x}$(a>0)的最大值大于等于0,
当x=$\frac{a}{6}$时,函数f(x)取最大值$\frac{\sqrt{3}}{6}$a-6,
故$\frac{\sqrt{3}}{6}$a-6≥0,
解得:a≥12$\sqrt{3}$,
故答案为:12$\sqrt{3}$
点评 本题以命题的真假判断与应用为载体,考查了函数的最值,函数的极值,函数的零点,函数的奇偶性等知识点,难度中档.

练习册系列答案
相关题目
16.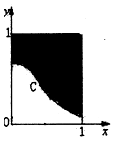 在如图所示的正方形中随机投掷10000个点,则落入阴影部分(曲线C为正态分布N(0,1)的密度曲线)的点的个数的估计值为( )
在如图所示的正方形中随机投掷10000个点,则落入阴影部分(曲线C为正态分布N(0,1)的密度曲线)的点的个数的估计值为( )
温馨提示:若X~N(μ,σ2),则P(μ-σ<X<μ+σ)=68.26%,P(μ-2σ<X<μ+2σ)=95.44%
 在如图所示的正方形中随机投掷10000个点,则落入阴影部分(曲线C为正态分布N(0,1)的密度曲线)的点的个数的估计值为( )
在如图所示的正方形中随机投掷10000个点,则落入阴影部分(曲线C为正态分布N(0,1)的密度曲线)的点的个数的估计值为( )温馨提示:若X~N(μ,σ2),则P(μ-σ<X<μ+σ)=68.26%,P(μ-2σ<X<μ+2σ)=95.44%
| A. | 7614 | B. | 6587 | C. | 6359 | D. | 3413 |
16.椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左焦点为F,若F关于直线$\sqrt{3}$x+y=0的对称点A是椭圆C上的点,则椭圆C的离心率为( )
| A. | $\sqrt{2}$-1 | B. | $\sqrt{3}$-1 | C. | $\sqrt{5}$-2 | D. | $\sqrt{6}$-2 |
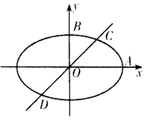 已知椭圆E:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率e=$\frac{\sqrt{3}}{2}$,且过点($\frac{\sqrt{3}}{2}$,$\frac{1}{4}$).
已知椭圆E:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率e=$\frac{\sqrt{3}}{2}$,且过点($\frac{\sqrt{3}}{2}$,$\frac{1}{4}$).