题目内容
已知直线C1：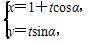
(t为参数)，圆C2：
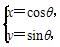(θ为参数)．
(1)当α＝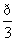
时，求C1与C2的交点坐标；
(2)过坐标原点O作C1的垂线，垂足为A，P为OA的中点．当α变化时，求P点轨迹的参数方程，并指出它是什么曲线．
[解析] (1)当α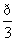＝时，C1的普通方程为y＝
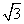(x－1)，C2的普通方程为x2＋y2＝1.
联立方程组
解得C1与C2的交点为(1,0)，(
，－
)．
(2)C1的普通方程为xsinα－ycosα－sinα＝0.
A点坐标为(sin2α，－cosαsinα)，
故当α变化时，P点轨迹的参数方程为
(α为参数)，
消去参数得P点轨迹的普通方程为(x－
)2＋y2＝
，
故P点轨迹是圆心为(
，0)，半径为的圆．
练习册系列答案
相关题目
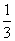x3－x，数列{an}满足条件：a1≥1，an＋1≥f ′(an＋1)．
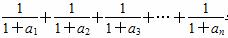与1的大小，并说明理由．
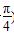)＝2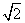
的距离为________．
＋
＝1的焦点为焦点，以直线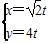
为渐近线的双曲线的参数方程为________________．
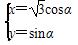(α为参数)，直线l：ρ(cosθ＋sinθ)＝4.
＋
的最小值为________．
＋
＋
的最大值为( )
B.
D.
