题目内容
盒中有6只晶体管，有2只次品，4只合格品，从中任取2次，每次一只；
（1）若取后放回，求取到的2只晶体管中恰有一只合格品的概率是多少？
（2）若取后不放回，求取到的2只晶体管中至少有一只合格概率是多少？
（3）若取后不放回，求取到的2只晶体管中至多有一只合格概率是多少？
（1）若取后放回，求取到的2只晶体管中恰有一只合格品的概率是多少？
（2）若取后不放回，求取到的2只晶体管中至少有一只合格概率是多少？
（3）若取后不放回，求取到的2只晶体管中至多有一只合格概率是多少？
考点：古典概型及其概率计算公式
专题：概率与统计
分析：（1）分别求出有放回的从中任取2次，抽取的情况总数，和取到的2只晶体管中恰有一只合格品的情况个数，代入古典概型概率计算公式，可得答案．
（2）分别求出不放回的从中任取2次，抽取的情况总数，和取到的2只晶体管中至少有一只合格品的情况个数，代入古典概型概率计算公式，可得答案．
（3）分别求出不放回的从中任取2次，抽取的情况总数，和取到的2只晶体管中至多有一只合格品的情况个数，代入古典概型概率计算公式，可得答案．
（2）分别求出不放回的从中任取2次，抽取的情况总数，和取到的2只晶体管中至少有一只合格品的情况个数，代入古典概型概率计算公式，可得答案．
（3）分别求出不放回的从中任取2次，抽取的情况总数，和取到的2只晶体管中至多有一只合格品的情况个数，代入古典概型概率计算公式，可得答案．
解答：
解：记4只合格品为A、B、C、D，2只次品为a、b；
（1）若取后放回，如表所示，共有36个基本事件，
…（3分）
其中，“取到的2只晶体管中恰有一只合格品”包含16个基本事件，由于每只晶体管被取到的可能性是相等的，由古典概型计算公式得：…（5分）
P{取到的2只晶体管中恰有一只合格品}=
=
； …（6分）
（2）若取后不放回，基本事件总数为30，其中“取到的2只晶体管中至少有一只合格”包含28个基本事件，故
P{取到的2只晶体管中至少有一只合格}=
=
； …（10分）
（3）若取后不放回，基本事件总数为30，其中“取到的2只晶体管中至多有一只合格”包含18个基本事件，故
P{取到的2只晶体管中至多有一只合格}=
=
． …（14分）
（1）若取后放回，如表所示，共有36个基本事件，
| 第二次 第一次 |
A | B | C | D | a | b |
| A | （A，A） | （A，B） | （A，C） | （A，D） | （A，a） | （A，b） |
| B | （B，A） | （B，B） | （B，C） | （B，D） | （B，a） | （B，b） |
| C | （C，A） | （C，B） | （C，C） | （C，D） | （C，a） | （C，b） |
| D | （D，A） | （D，B） | （D，C） | （D，D） | （D，a） | （D，b） |
| a | （a，A） | （a，B） | （a，C） | （a，D） | （a，a） | （a，b） |
| b | （b，A） | （b，B） | （b，C） | （b，D） | （b，a） | （b，b） |
其中，“取到的2只晶体管中恰有一只合格品”包含16个基本事件，由于每只晶体管被取到的可能性是相等的，由古典概型计算公式得：…（5分）
P{取到的2只晶体管中恰有一只合格品}=
| 16 |
| 36 |
| 4 |
| 9 |
（2）若取后不放回，基本事件总数为30，其中“取到的2只晶体管中至少有一只合格”包含28个基本事件，故
P{取到的2只晶体管中至少有一只合格}=
| 28 |
| 30 |
| 14 |
| 15 |
（3）若取后不放回，基本事件总数为30，其中“取到的2只晶体管中至多有一只合格”包含18个基本事件，故
P{取到的2只晶体管中至多有一只合格}=
| 18 |
| 30 |
| 9 |
| 15 |
点评：本题考查的知识点是古典概型概率计算公式，其中熟练掌握利用古典概型概率计算公式求概率的步骤，是解答的关键．
练习册系列答案
相关题目
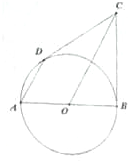如图，AB为圆O的直径，BC与圆O相切于点B，D为圆O上的一点，AD∥OC，连接CD．