题目内容
己知f(x)=
是奇函数,
(1)求a的值;
(2)判断f(x)的单调性,x∈R;
(3)若方程f(x)=m(m>0)在(-∞,0)上有解,求证:-
<f(m)<0.
| a•2x+a-2 |
| 2x |
(1)求a的值;
(2)判断f(x)的单调性,x∈R;
(3)若方程f(x)=m(m>0)在(-∞,0)上有解,求证:-
| 1 |
| 3 |
考点:奇偶性与单调性的综合,函数奇偶性的性质
专题:综合题,函数的性质及应用
分析:(1)根据函数f(x)为定义域为R的奇函数,则f(0)=0,代入解析式可求出a的值;
(2)y=
是R上的减函数,可得f(x)=1-
是R上的增函数;
(3)先确定1>m>0,即可得出结论.
(2)y=
| 1 |
| 2x |
| 1 |
| 2x |
(3)先确定1>m>0,即可得出结论.
解答:
(1)解:f(x)的定义域为R,且为奇函数,∴f(0)=0,
∴a=1;
(2)解:f(x)=1-
,∵y=
是R上的减函数,∴f(x)=1-
是R上的增函数;
(3)证明:∵方程f(x)=m在(-∞,0)上有解,
∴1>m>0,∴-
<f(m)<0,
∴-
<f(m)<0.
∴a=1;
(2)解:f(x)=1-
| 1 |
| 2x |
| 1 |
| 2x |
| 1 |
| 2x |
(3)证明:∵方程f(x)=m在(-∞,0)上有解,
∴1>m>0,∴-
| 1 |
| 2 |
∴-
| 1 |
| 3 |
点评:本题主要考查了函数的奇偶性,以及函数的单调性和函数的值域,属于中档题.

练习册系列答案
 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案
相关题目
(理)已知不等式(2a-b-c)(a-c)•2n≥(a-b)(b-c)(t•2n+1)对任意a>b>c及n∈N恒成立,则实数t的取值范围为 ( )
A、(-∞,4
| ||
B、(-∞,2+2
| ||
C、[4
| ||
D、[2+2
|
命题“?x∈(0,+∞),x3-x2+1≥0,”的否定是( )
| A、?x∈(0,+∞),x3-x2+1≤0 |
| B、?x∈(0,+∞),x3-x2+1≤0 |
| C、?x∈(0,+∞),x3-x2+1<0 |
| D、?x∈(0,-∞),x3-x2+1<0 |
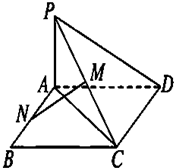 如图四边形ABCD是矩形,PA⊥平面ABCD,PA=AD,M、N分别是PC、AB的中点.
如图四边形ABCD是矩形,PA⊥平面ABCD,PA=AD,M、N分别是PC、AB的中点.