题目内容
某校高二(1)班举行游戏中,有甲、乙两个盒子,这两个盒子中各装有大小、形状完全相同,但颜色不同的8个小球,其中甲盒子中装有6个红球、2个白球,乙盒子中装有7个黄球、1个黑球,现进行摸球游戏,游戏规则:从甲盒子中摸一个红球记4分,摸出一个白球记-1分;从乙盒子中摸出一个黄球记6分,摸出一个黑球记-2分.
(1)如果每次从甲盒子摸出一个球,记下颜色后再放回,求连续从甲盒子中摸出3个球所得总分(3次得分的总和)不少于5分的概率;
(2)设X(单位:分)为分别从甲、乙盒子中各摸一个球所获得的总分,求X的数学期望.
(1)如果每次从甲盒子摸出一个球,记下颜色后再放回,求连续从甲盒子中摸出3个球所得总分(3次得分的总和)不少于5分的概率;
(2)设X(单位:分)为分别从甲、乙盒子中各摸一个球所获得的总分,求X的数学期望.
考点:离散型随机变量的期望与方差,古典概型及其概率计算公式
专题:概率与统计
分析:(1)设连续从甲盒子中摸出的3个球中,红球有x个,则白球有3-x个,由题意知4x-(3-x)≥5,由此能求出连续从甲盒子中摸出3个球所得总分(3次得分的总和)不少于5分的概率.
(2)由题意知X可能取值分别为10,5,2,-3,分别求出相应的概率,由此能求出X的数学期望.
(2)由题意知X可能取值分别为10,5,2,-3,分别求出相应的概率,由此能求出X的数学期望.
解答:
解:(1)设连续从甲盒子中摸出的3个球中,
红球有x个,则白球有3-x个,
由题意知4x-(3-x)≥5,
解得x≥
,
∵x∈N*,且x≤3,∴x=2或x=3,
∴连续从甲盒子中摸出3个球所得总分(3次得分的总和)不少于5分的概率:
p=
(
)2×
+(
)3=
.
(2)由题意知X可能取值分别为10,5,2,-3,
∵每次摸球相互独立,
∴P(X=10)=
×
=
,
P(X=5)=
×
=
,
P(X=2)=
×
=
,
P(X=-1)=
×
=
,
∴X的数学期望EX=10×
+5×
+2×
+(-3)×
=
.
红球有x个,则白球有3-x个,
由题意知4x-(3-x)≥5,
解得x≥
| 8 |
| 5 |
∵x∈N*,且x≤3,∴x=2或x=3,
∴连续从甲盒子中摸出3个球所得总分(3次得分的总和)不少于5分的概率:
p=
| C | 2 3 |
| 3 |
| 4 |
| 1 |
| 4 |
| 3 |
| 4 |
| 27 |
| 32 |
(2)由题意知X可能取值分别为10,5,2,-3,
∵每次摸球相互独立,
∴P(X=10)=
| 6 |
| 8 |
| 7 |
| 8 |
| 21 |
| 32 |
P(X=5)=
| 2 |
| 8 |
| 7 |
| 8 |
| 7 |
| 32 |
P(X=2)=
| 6 |
| 8 |
| 1 |
| 8 |
| 3 |
| 32 |
P(X=-1)=
| 2 |
| 8 |
| 1 |
| 8 |
| 1 |
| 32 |
∴X的数学期望EX=10×
| 21 |
| 32 |
| 7 |
| 32 |
| 3 |
| 32 |
| 1 |
| 32 |
| 31 |
| 4 |
点评:本题考查概率的求法,考查离散型分布列的数学期望的求法,解题时要认真审题,是中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目

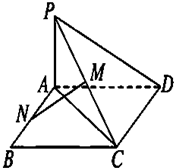 如图四边形ABCD是矩形,PA⊥平面ABCD,PA=AD,M、N分别是PC、AB的中点.
如图四边形ABCD是矩形,PA⊥平面ABCD,PA=AD,M、N分别是PC、AB的中点.