题目内容
（Ⅰ）求值：tan45°+tan15°+
tan45°•tan15°
（Ⅱ）某同学在学习中发现，以下两个式子：
①tan13°+tan47°+
tan13°•tan47°；②tan（-20°）+tan80°+
tan（-20°）•tan80°的值与（Ⅰ）中计算的结果相同，请你根据这三个式子的结果，将该同学的发现推广为三角恒等式，并证明你的结论．
| 3 |
（Ⅱ）某同学在学习中发现，以下两个式子：
①tan13°+tan47°+
| 3 |
| 3 |
考点：两角和与差的正切函数,归纳推理
专题：三角函数的求值
分析：（Ⅰ）易求tan45°=1，tan15°=2-
，代入所求关系式，即可得到答案为
；
（Ⅱ）若α+β=60°，则tanα+tanβ+
tanαtanβ=
，利用两角和的正切公式tan（α+β）=
，可得tanα+tanβ=tan（α+β）（1-tanαtanβ），将α+β=60°，代入计算即可证得结论成立．
| 3 |
| 3 |
（Ⅱ）若α+β=60°，则tanα+tanβ+
| 3 |
| 3 |
| tanα+tanβ |
| 1-tanαtanβ |
解答：
解：（ I）tan45°=1，tan15°=tan（45°-30°）=
=
=2-
，
所以原式=1+2-
+
（2-
）=
-------------------------------------------------（5分）
（注：用第二问中的证明方法去计算也给分）
（ II）若α+β=60°，则tanα+tanβ+
tanαtanβ=
，------------------（6分）
证明：因为tan（α+β）=
，所以tanα+tanβ=tan（α+β）（1-tanαtanβ），
左边=tan（α+β）（1-tanαtanβ）+
tanαtanβ
=tan60°（1-tanαtanβ）+
tanαtanβ
=
（1-tanαtanβ）+
tanαtanβ
=
，---------------------------（10分）
| tan45°-tan30° |
| 1+tan45°tan30° |
1-
| ||||
1+1×
|
| 3 |
所以原式=1+2-
| 3 |
| 3 |
| 3 |
| 3 |
（注：用第二问中的证明方法去计算也给分）
（ II）若α+β=60°，则tanα+tanβ+
| 3 |
| 3 |
证明：因为tan（α+β）=
| tanα+tanβ |
| 1-tanαtanβ |
左边=tan（α+β）（1-tanαtanβ）+
| 3 |
=tan60°（1-tanαtanβ）+
| 3 |
=
| 3 |
| 3 |
=
| 3 |
点评：本题考查两角和与差的正切函数，着重考查推理运算及证明能力，属于中档题．
练习册系列答案
阅读快车系列答案
相关题目
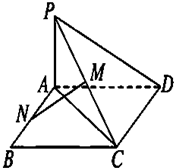如图四边形ABCD是矩形，PA⊥平面ABCD，PA=AD，M、N分别是PC、AB的中点．