题目内容
11.某车间20名工人年龄数据如表:| 年龄(岁) | 19 | 24 | 26 | 30 | 34 | 35 | 40 | 合计 |
| 工人数(人) | 1 | 3 | 3 | 5 | 4 | 3 | 1 | 20 |
(Ⅱ) 以十位数为茎,个位数为叶,作出这20名工人年龄的茎叶图;
(Ⅲ) 从年龄在24和26的工人中随机抽取2人,求这2人均是24岁的概率.
分析 (Ⅰ)利用车间20名工人年龄数据表能求出这20名工人年龄的众数和平均数.
(Ⅱ)利用车间20名工人年龄数据表能作出茎叶图.
(Ⅲ) 记年龄为24岁的三个人为A1,A2,A3;年龄为26岁的三个人为B1,B2,B3,利用列举法能求出这2人均是24岁的概率.
解答 (本小题满分12分)
解 (Ⅰ) 由题意可知,这20名工人年龄的众数是30,--------------------------------(2分)
这20名工人年龄的平均数为$\overline x$=$\frac{1}{20}$(19+3×28+3×29+5×30+4×31+3×32+40)=30,------------------------------(4分)
(Ⅱ) 这20名工人年龄的茎叶图如图所示: ------------------------------------------(7分)
------------------------------------------(7分)
(Ⅲ) 记年龄为24岁的三个人为A1,A2,A3;年龄为26岁的三个人为B1,B2,B3,
则从这6人中随机抽取2人的所有可能为
{A1,A2},{A1,A3},{A2,A3},{A1,B1},{A1,B2},
{A1,B3},{A2,B1},{A2,B2},{A2,B,3},{A3,B1},
{A3,B2},{A,3,B3},{B1,B2},{B1,B3},{B2,B3}共15种.----------------------(9分)
满足题意的有{A1,A2},{A1,A3},{A2,A3}3种,-------------------------------------(11分)
故所求的概率为P=$\frac{3}{15}=\frac{1}{5}$-----------------------------------------------------------(12分)
点评 本题考查众数、平均数、概率的求法,考查茎叶图的作法,是基础题,解题时要认真审题,注意列举法的合理运用.

 开心蛙状元测试卷系列答案
开心蛙状元测试卷系列答案| A. | [0,$\frac{1}{8}$] | B. | [-1,0]∪(0,$\frac{1}{8}$] | C. | [-1,0] | D. | [-1,$\frac{1}{8}$] |
| A. | 3 | B. | 3i | C. | 2 | D. | 2i |
| A. | $-\frac{1}{2}$ | B. | $-\frac{{\sqrt{3}}}{2}$ | C. | $\frac{1}{2}$ | D. | $\frac{{\sqrt{3}}}{2}$ |
| A. | $\frac{a+b}{2}$ | B. | $\sqrt{ab}$ | C. | $\sqrt{(a+1)(b+1)}-1$ | D. | $\sqrt{(a+1)(b+1)}+1$ |
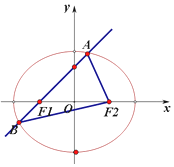 如图,已知中心在坐标原点的椭圆C,F1,F2 分别为椭圆的左、右焦点,右顶点到右准线的距离为2,离心率为$\frac{1}{2}$.过椭圆的左焦点F1 任意作一条直线l 与椭圆交于A,B 两点.设A(x1,y1),B(x2,y2).
如图,已知中心在坐标原点的椭圆C,F1,F2 分别为椭圆的左、右焦点,右顶点到右准线的距离为2,离心率为$\frac{1}{2}$.过椭圆的左焦点F1 任意作一条直线l 与椭圆交于A,B 两点.设A(x1,y1),B(x2,y2).