题目内容
根据条件确定角α属于哪个象限的角或角的终边位置.
(1)sin(2kπ+α)>0(k∈Z),且cosα≤0;
(2)(
)sin2θ>1,且tanθ•sinθ<0.
(1)sin(2kπ+α)>0(k∈Z),且cosα≤0;
(2)(
| 1 |
| 2 |
考点:三角函数值的符号
专题:三角函数的求值
分析:(1)由诱导公式化简sin(2kπ+α)>0,再由三角函数值的符号判断出α所在的象限,注意象限界角;
(2)由指数函数的性质、商的关系化简后,再由三角函数值的符号判断出α所在的象限,注意象限界角.
(2)由指数函数的性质、商的关系化简后,再由三角函数值的符号判断出α所在的象限,注意象限界角.
解答:
解:(1)由sin(2kπ+α)>0(k∈Z)得,sinα>0,
则α是第一或二象限角或终边在y轴的正半轴上,
由cosα≤0得,α是第二或三象限角或终边在y轴上,
综上可得,α是第二象限角或终边在y轴的正半轴上;
(2)由(
)sin2θ>1=(
)0得,sin2θ<0,则2sinθcosθ<0,①
由tanθ•sinθ<0得
•sinθ<0,则cosθ<0,
则θ是第二或三象限角或终边在x轴的负半轴上,
代入①得sinθ>0,则是θ第一或二象限角或终边在y轴的正半轴上,
综上可得,θ是第二象限角.
则α是第一或二象限角或终边在y轴的正半轴上,
由cosα≤0得,α是第二或三象限角或终边在y轴上,
综上可得,α是第二象限角或终边在y轴的正半轴上;
(2)由(
| 1 |
| 2 |
| 1 |
| 2 |
由tanθ•sinθ<0得
| sinθ |
| cosθ |
则θ是第二或三象限角或终边在x轴的负半轴上,
代入①得sinθ>0,则是θ第一或二象限角或终边在y轴的正半轴上,
综上可得,θ是第二象限角.
点评:本题考查三角函数值的符号,诱导公式和商的关系,以及指数函数的性质,注意特殊情况:象限界角.

练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
已知正数x、y、z满足x2+y2+z2=1,则S=
的最小值为( )
| 1+z |
| 2xyz |
| A、3 | ||||
B、
| ||||
| C、4 | ||||
D、2(
|
如图所示,直线l1,l2,l3的斜率分别为k1,k2,k3,则( )
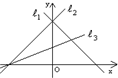

| A、k1<k2<k3 |
| B、k3<k1<k2 |
| C、k1<k3<k2 |
| D、k3<k2<k1 |