题目内容
设函数f(x)=1+
的最大值为M,最小值为N,则M+N= .
| x |
| x2+1 |
考点:基本不等式
专题:不等式的解法及应用
分析:对x分类讨论,变形利用基本不等式的性质即可得出.
解答:
解:当x>0时,f(x)=1+
≤1+
=
,当且仅当x=1时取等号.
当x<0时,f(x)=1+
=1+
≥1-
=
,当且仅当x=-1时取等号.
当x=0时,f(0)=1.
综上可得:函数f(x)=1+
的最大值为M=
,最小值为N=
,则M+N=2.
故答案为:2.
| 1 | ||
x+
|
| 1 |
| 2 |
| 3 |
| 2 |
当x<0时,f(x)=1+
| 1 | ||
x+
|
| 1 | ||
-(-x+
|
| 1 |
| 2 |
| 1 |
| 2 |
当x=0时,f(0)=1.
综上可得:函数f(x)=1+
| x |
| x2+1 |
| 3 |
| 2 |
| 1 |
| 2 |
故答案为:2.
点评:本题考查了基本不等式的性质、分类讨论思想方法,考查了推理能力与计算能力,属于基础题.

练习册系列答案
 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案
相关题目
已知空间直角坐标系中点A(1,0,0),B(2,0,1),C(0,1,2),则平面ABC的一个法向量为( )
| A、(-1,-3,2) |
| B、(1,3,-1) |
| C、(1,3,1) |
| D、(-1,3,1) |
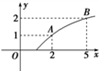 已知函数f(x)=log3(ax+b)的部分图象如图所示.
已知函数f(x)=log3(ax+b)的部分图象如图所示.