题目内容
已知函数f(x)=-x+log2
,其定义域为(-1,1).
(1)求f(
)+f(-
)的值;
(2)判断函数f(x)在定义域上的单调性并给出证明.
| 1-x |
| 1+x |
(1)求f(
| 1 |
| 2014 |
| 1 |
| 2014 |
(2)判断函数f(x)在定义域上的单调性并给出证明.
考点:函数单调性的判断与证明,函数的定义域及其求法,函数的值
专题:函数的性质及应用
分析:(1)用定义判断函数f(x)是定义域(-1,1)上的奇函数,从而求出f(
)+f(-
)的值;
(2)用单调性的定义判断并证明函数f(x)在定义域上的单调性.
| 1 |
| 2014 |
| 1 |
| 2014 |
(2)用单调性的定义判断并证明函数f(x)在定义域上的单调性.
解答:
解:(1)∵函数f(x)=-x+log2
,定义域为(-1,1);
∴任取x∈(-1,1),
有f(-x)=x+log2
=x-log2
=-f(x),
∴f(x)是定义域(-1,1)上的奇函数;
∴f(
)+f(-
)=0;
(2)函数f(x)在定义域(-1,1)上是减函数;
证明如下:任取x1,x2∈(-1,1),且x1<x2;
∴f(x1)-f(x2)=(-x1+log2
)-(-x2+log2
)
=(x2-x1)+log2
=(x2-x1)+log2
,
∵-1<x1<x2<1,
∴x2-x1>0,
∴1-x1x2+x2-x1>1-x1x2+x1-x2>0,
∴log2
>0,
∴f(x1)-f(x2)>0,
即f(x1)>f(x2);
∴f(x)是定义域(-1,1)上的减函数.
| 1-x |
| 1+x |
∴任取x∈(-1,1),
有f(-x)=x+log2
| 1+x |
| 1-x |
| 1-x |
| 1+x |
∴f(x)是定义域(-1,1)上的奇函数;
∴f(
| 1 |
| 2014 |
| 1 |
| 2014 |
(2)函数f(x)在定义域(-1,1)上是减函数;
证明如下:任取x1,x2∈(-1,1),且x1<x2;
∴f(x1)-f(x2)=(-x1+log2
| 1-x1 |
| 1+x1 |
| 1-x2 |
| 1+x2 |
=(x2-x1)+log2
| (1-x1)(1+x2) |
| (1+x1)(1-x2) |
=(x2-x1)+log2
| 1-x1x2+x2-x1 |
| 1-x1x2+x1-x2 |
∵-1<x1<x2<1,
∴x2-x1>0,
∴1-x1x2+x2-x1>1-x1x2+x1-x2>0,
∴log2
| 1-x1x2+x2-x1 |
| 1-x1x2+x1-x2 |
∴f(x1)-f(x2)>0,
即f(x1)>f(x2);
∴f(x)是定义域(-1,1)上的减函数.
点评:本题考查了用定义来判断和证明函数的单调性与奇偶性的问题,是基础题目.

练习册系列答案
 名师点拨卷系列答案
名师点拨卷系列答案
相关题目
某种放射性元素m克,其衰变函数为y=m•ekx,100年后只剩原来的一半,现有这种元素1克,3年后,剩下( )
| A、0.015g | |||
| B、(1-0.5%)3g | |||
| C、0.925g | |||
D、
|
 为了解某年级女生五十米短跑情况,从该年级中随机抽取8名女生进行五十跑测试,她们的测试成绩(单位:秒)的茎叶图(以整数部分为茎,小数部分为叶)如图所示.由此可估计该年级女生五十米跑成绩及格(及格成绩为9.4秒)的概率为( )
为了解某年级女生五十米短跑情况,从该年级中随机抽取8名女生进行五十跑测试,她们的测试成绩(单位:秒)的茎叶图(以整数部分为茎,小数部分为叶)如图所示.由此可估计该年级女生五十米跑成绩及格(及格成绩为9.4秒)的概率为( )| A、0.375 | B、0.625 |
| C、0.5 | D、0.125 |
下列函数中,在区间(0,+∞)上是增函数的是( )
| A、y=-x2 | ||
| B、y=x2-x+2 | ||
C、y=(
| ||
D、y=log0.3
|
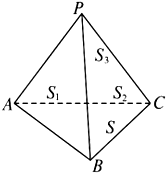 在△ABC中,射影定理可以表示为a=bcosC+ccosB,其中a,b,c依次为角A、B、C的对边.类比以上定理,如图,在四面体P-ABC中,S1、S2、S3、S分别表示△PAB、△PBC、△PCA、△ABC的面积,α、β、γ依次表示面PAB、面PBC、面PCA与底面ABC所成角的大小,我们猜想将射影定理类比推广到三维空间,其表现形式应为
在△ABC中,射影定理可以表示为a=bcosC+ccosB,其中a,b,c依次为角A、B、C的对边.类比以上定理,如图,在四面体P-ABC中,S1、S2、S3、S分别表示△PAB、△PBC、△PCA、△ABC的面积,α、β、γ依次表示面PAB、面PBC、面PCA与底面ABC所成角的大小,我们猜想将射影定理类比推广到三维空间,其表现形式应为