题目内容
设a∈R，试讨论关于x的方程lg（x-1）+lg（3-x）=lg（a-x）的实根个数．
考点：根的存在性及根的个数判断
专题：函数的性质及应用
分析：由对数的含义及运算法则，转化为二次方程的解得问题处理即可，注意定义域．
解答：
解：由题意x-1＞0且3-x＞0，所以1＜x＜3，
又lg（x-1）+lg（3-x）=lg（x-1）（3-x）=lg（a-x）
所以（x-1）（3-x）=a-x在1＜x＜3上有两个实根，
即判断x2-5x+a+3=0在（1，3）上个实根的个数．
所以a=-x2+5x-3，x∈（1，3），
令f（x）=-x2+5x-3，x∈（1，3），
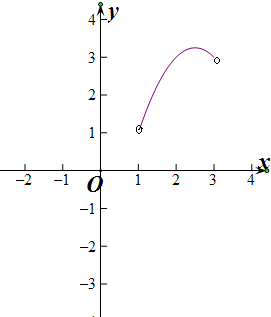
f（1）=1，f（3）=3，f（
）=
，
当1＜a≤3，或a=
时，方程有1个实根，
当3＜a＜
时，方程有2个实根，
当a≤1或a＞
时，方程有无实根，
又lg（x-1）+lg（3-x）=lg（x-1）（3-x）=lg（a-x）
所以（x-1）（3-x）=a-x在1＜x＜3上有两个实根，
即判断x2-5x+a+3=0在（1，3）上个实根的个数．
所以a=-x2+5x-3，x∈（1，3），
令f（x）=-x2+5x-3，x∈（1，3），
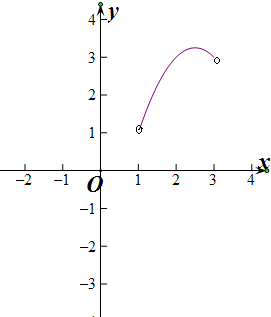
f（1）=1，f（3）=3，f（
| 5 |
| 2 |
| 13 |
| 4 |
当1＜a≤3，或a=
| 13 |
| 4 |
当3＜a＜
| 13 |
| 4 |
当a≤1或a＞
| 13 |
| 4 |
点评：本题考查二次方程实根分布问题、对数的运算法则，同时考查等价转化思想，属于中档题．
练习册系列答案
相关题目
已知Rt△ABC，∠C=90°，CA=3，CB=4，点D、E在AB上，满足
=
，
=-
，则
•
=（ ）
| AD |
| 1 |
| 3 |
| AB |
| BE |
| 1 |
| 4 |
| AB |
| CE |
| CD |
A、
| ||
B、
| ||
C、
| ||
D、
|
若f（x）为定义在R上的偶函数，且f（x+2）=f（x），当x∈[0，1]时，f（x）=x2+1，则当 x∈[3，5]时，f（x）=（ ）
| A、（x+3）2+1 |
| B、（x-3）2+1 |
| C、（x-4）2+1 |
| D、（x-5）2+1 |
已知a，b，c分别是△ABC的三内角A，B，C所对的边，若a=1，b=
，B=
，则sinC的值为（ ）
| 3 |
| π |
| 3 |
| A、1 | ||||
B、
| ||||
C、
| ||||
D、
|