题目内容
若f(x)为定义在R上的偶函数,且f(x+2)=f(x),当x∈[0,1]时,f(x)=x2+1,则当 x∈[3,5]时,f(x)=( )
| A、(x+3)2+1 |
| B、(x-3)2+1 |
| C、(x-4)2+1 |
| D、(x-5)2+1 |
考点:函数奇偶性的性质
专题:函数的性质及应用
分析:f(x)是个周期为2的周期函数,且是个偶函数,先求当 x∈[-1,0]时,f(x)的表达式;再求当 x∈[3,5]时的表达式.
解答:
解:由题意知,函数y=f(x)是周期为2的周期函数,且是偶函数,
∴f(x)=f(-x)
∵当 x∈[0,1]时,f(x)=x2+1,
当 x∈[-1,0]时,f(x)=f(-x)=(-x)2+1)=x2+1,
∴当 x∈[-1,1]时,f(x)=x2+1,
当 x∈[3,5]时,x-4∈[-1,1]
∴f(x)=f(x-4)=(x-4)2+1,
故选:D.
∴f(x)=f(-x)
∵当 x∈[0,1]时,f(x)=x2+1,
当 x∈[-1,0]时,f(x)=f(-x)=(-x)2+1)=x2+1,
∴当 x∈[-1,1]时,f(x)=x2+1,
当 x∈[3,5]时,x-4∈[-1,1]
∴f(x)=f(x-4)=(x-4)2+1,
故选:D.
点评:本题考查的知识点是函数的奇偶性和函数的周期性,其中根据函数的奇偶性,求出函数的解析式是解答的关键.

练习册系列答案
 名师伴你成长课时同步学练测系列答案
名师伴你成长课时同步学练测系列答案
相关题目
圆O1:x2+y2-2x=0和圆O2:x2+y2-4y=0的公共弦长为( )
A、
| ||||
B、
| ||||
| C、3 | ||||
D、
|
若平面
,
满足|
+
|=1,
+
平行于y轴,
=(2,-1),则
=( )
| a |
| b |
| a |
| b |
| a |
| b |
| b |
| a |
| A、(-1,1) |
| B、(-2,2) |
| C、(-1,1)或(-3,1) |
| D、(-2,2)或(-2,0) |
在钝角△ABC中,a=1,b=2,则最大边c的取值范围是( )
| A、1<c<3 | ||
| B、2<c<3 | ||
C、
| ||
D、2
|
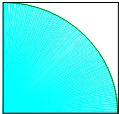 如图:在边长为2正方形内有一扇形(见阴影部分),点P随意等可能落在正方形内,
如图:在边长为2正方形内有一扇形(见阴影部分),点P随意等可能落在正方形内,