题目内容
已知函数f(x)=ax+lnx,g(x)=ex,a∈R.
(1)求f(x)的单调区间;(2)若不等式g(x)<
有解,求实数m的取值范围;
(3)定义:对于函数y=F(x)和y=G(x)在其公共定义域内的任意实数x0,称|F(x0)-G(x0)|的值为两函数在x0处的差值.证明:当a=0时,函数y=f(x)和f=g(x)在其公共定义域内的所有差值都大于2.
(1)求f(x)的单调区间;(2)若不等式g(x)<
| x-m | ||
|
(3)定义:对于函数y=F(x)和y=G(x)在其公共定义域内的任意实数x0,称|F(x0)-G(x0)|的值为两函数在x0处的差值.证明:当a=0时,函数y=f(x)和f=g(x)在其公共定义域内的所有差值都大于2.
考点:利用导数研究函数的极值
专题:导数的综合应用
分析:(1)先求出其导函数,以及导函数大于0,小于0对应的区间即可求函数f(x)的单调区间;
(2)因为关于x的不等式g(x)<
有解,将问题转化为ex
<x-m有解,利用常数分离法进行求解;
(3)当a=0时,f(x)=lnx,f(x)与g(x)的公共定义域为(0,+∞),由于|f(x)-g(x)|=|lnx-ex|=ex-lnx=ex-x-(lnx-x),设m(x)=ex-x,利用导数研究其单调性得出m(x)>m(0)=1,同样地,设n(x)=lnx-x,x∈(0,+∞),得到n(x)≤n(1)=-1,从而有|f(x)-g(x)|=m(x)-n(x)>1-(-1)=2,即在其公共定义域内的所有差值都大干2.
(2)因为关于x的不等式g(x)<
| x-m | ||
|
| x |
(3)当a=0时,f(x)=lnx,f(x)与g(x)的公共定义域为(0,+∞),由于|f(x)-g(x)|=|lnx-ex|=ex-lnx=ex-x-(lnx-x),设m(x)=ex-x,利用导数研究其单调性得出m(x)>m(0)=1,同样地,设n(x)=lnx-x,x∈(0,+∞),得到n(x)≤n(1)=-1,从而有|f(x)-g(x)|=m(x)-n(x)>1-(-1)=2,即在其公共定义域内的所有差值都大干2.
解答:
解:(1)函数f(x)的定义域为(0,+∞),f′(x)=(ax+lnx)′=a+
,
①当a=0时,f′(x)>0,∴f(x)在(0,+∞)为单调递增函数;
②当a<0时,f′(x)=0,得x=-
,当x∈(0,-
)时,f′(x)>0;当x∈(-
,+∞)时,f′(x)<0;
∴f(x)在(0,-
)为单调递增函数;在(-
,+∞)为单调递减函数;
③当a>0时,f′(x)=0,得x=-
,当x∈(0,-
)时,f′(x)<0;当x∈(-
,+∞)时,f′(x)>0;
∴f(x)在(0,-
)为单调递减函数;在(-
,+∞)为单调递增函数.
(2)由题意,不等式g(x)<
有解,即ex
<x-m有解,
因此只须m<x-ex
,x∈(0,+∞),
设h(x)=x-ex
,x∈(0,+∞),h′(x)=1-ex(
+
),
因为
+
≥2
=
>1,且ex>1,∴1-ex(
+
)<0,故h(x)在(0,+∞)上是减函数,
∴h(x)<h(0)=0,故m<0.
(3)当a=0时,f(x)=lnx,f(x)与g(x)的公共定义域为(0,+∞),
|f(x)-g(x)|=|lnx-ex|=ex-lnx=ex-x-(lnx-x),设m(x)=ex-x,x∈(0,+∞),
因为m′(x)=ex-1>0,m(x)在(0,+∞)上是增函数,m(x)>m(0)=1,
又设n(x)=lnx-x,x∈(0,+∞),
因为n′(x)=
-1,当x∈(0,1)时,n′(x)>0,n(x)在(0,1)上是增函数,
当x∈(1,+∞)时,n′(x)<0,n(x)在(1.+∞)上是减函数,
∴当x=1时,n(x)取得极大值点,
即n(x)≤n(1)=-1,故|f(x)-g(x)|=m(x)-n(x)>1-(-1)=2,
即在其公共定义域内的所有差值都大干2.
| 1 |
| x |
①当a=0时,f′(x)>0,∴f(x)在(0,+∞)为单调递增函数;
②当a<0时,f′(x)=0,得x=-
| 1 |
| a |
| 1 |
| a |
| 1 |
| a |
∴f(x)在(0,-
| 1 |
| a |
| 1 |
| a |
③当a>0时,f′(x)=0,得x=-
| 1 |
| a |
| 1 |
| a |
| 1 |
| a |
∴f(x)在(0,-
| 1 |
| a |
| 1 |
| a |
(2)由题意,不等式g(x)<
| x-m | ||
|
| x |
因此只须m<x-ex
| x |
设h(x)=x-ex
| x |
| x |
| 1 | ||
2
|
因为
| x |
| 1 | ||
2
|
|
| 2 |
| x |
| 1 | ||
2
|
∴h(x)<h(0)=0,故m<0.
(3)当a=0时,f(x)=lnx,f(x)与g(x)的公共定义域为(0,+∞),
|f(x)-g(x)|=|lnx-ex|=ex-lnx=ex-x-(lnx-x),设m(x)=ex-x,x∈(0,+∞),
因为m′(x)=ex-1>0,m(x)在(0,+∞)上是增函数,m(x)>m(0)=1,
又设n(x)=lnx-x,x∈(0,+∞),
因为n′(x)=
| 1 |
| x |
当x∈(1,+∞)时,n′(x)<0,n(x)在(1.+∞)上是减函数,
∴当x=1时,n(x)取得极大值点,
即n(x)≤n(1)=-1,故|f(x)-g(x)|=m(x)-n(x)>1-(-1)=2,
即在其公共定义域内的所有差值都大干2.
点评:本题考查利用导数求函数的单调区间的方法,求函数的导数以及利用导数研究函数的极值.注意函数的定义域,此题是一道中档题,考查学生计算能力.

练习册系列答案
相关题目
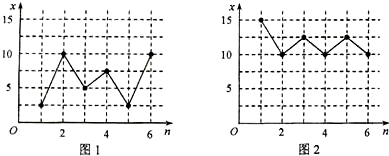
已知图1、图2分别表示A、B两城市某月1日至6日当天最低气温的数据折线图(其中横轴n表示日期,纵轴x表示气温),记A、B两城市这6天的最低气温平均数分别为
和
,标准差分别为sA和sB,则它们的大小关系是( )
. |
| xA |
. |
| xB |

A、
| ||||
B、
| ||||
C、
| ||||
D、
|
若平面
,
满足|
+
|=1,
+
平行于y轴,
=(2,-1),则
=( )
| a |
| b |
| a |
| b |
| a |
| b |
| b |
| a |
| A、(-1,1) |
| B、(-2,2) |
| C、(-1,1)或(-3,1) |
| D、(-2,2)或(-2,0) |