题目内容
1.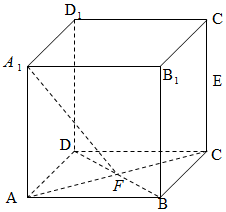 如图:已知在正方体ABCD-A1B1C1D1中,E是CC1的中点,F是AC,BD的交点.求A1F与B1E所成角的余弦值.
如图:已知在正方体ABCD-A1B1C1D1中,E是CC1的中点,F是AC,BD的交点.求A1F与B1E所成角的余弦值.
分析 如图所示,建立空间直角坐标系.利用cos<$\overrightarrow{F{A}_{1}}$,$\overrightarrow{E{B}_{1}}$>=$\frac{\overrightarrow{F{A}_{1}}•\overrightarrow{E{B}_{1}}}{|\overrightarrow{F{A}_{1}}|•|\overrightarrow{E{B}_{1}}|}$即可得出.
解答 解:如图所示,建立空间直角坐标系.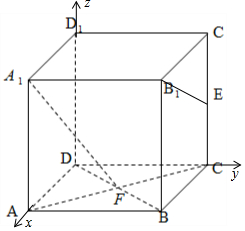
不妨设AB=2,则D(0,0,0),A1(2,0,2),F(1,1,0),
B1(2,2,2),E(0,2,1).
$\overrightarrow{F{A}_{1}}$=(1,-1,2),$\overrightarrow{E{B}_{1}}$=(2,0,1),
∴cos<$\overrightarrow{F{A}_{1}}$,$\overrightarrow{E{B}_{1}}$>=$\frac{\overrightarrow{F{A}_{1}}•\overrightarrow{E{B}_{1}}}{|\overrightarrow{F{A}_{1}}|•|\overrightarrow{E{B}_{1}}|}$=$\frac{4}{\sqrt{6}×\sqrt{5}}$=$\frac{2\sqrt{30}}{15}$,
∴A1F与B1E所成角的余弦值为$\frac{2\sqrt{30}}{15}$.
点评 本题考查了建立空间直角坐标系、利用向量夹角公式球异面直线的夹角,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 科学实验活动册系列答案
科学实验活动册系列答案
相关题目
19.(文)已知x,y满足(1+i)+(2-3i)=a+bi,则a,b分别等于( )
| A. | 3,-2 | B. | 3,2 | C. | 3,-3 | D. | -1,4 |
12.已知复数z=(a-4)+(a+2)i(a∈R),则“a=2”是“z为纯虚数”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 既不充分也不必要条件 | D. | 充要条件 |
13.在等比数列{an}中,已知${a_1}+{a_2}=-\frac{3}{2},{a_4}+{a_5}=12$,则数列是( )
| A. | 递增数列 | B. | 递减数列 | C. | 摆动数列 | D. | 常数列 |
11.函数$f(x)=3sin(2x+\frac{π}{2})$是( )
| A. | 周期为$\frac{π}{2}$的奇函数 | B. | 周期为$\frac{π}{2}$的偶函数 | ||
| C. | 周期为π的奇函数 | D. | 周期为π的偶函数 |