题目内容
9.已知函数$f(x)=\frac{2}{x}-{x^m}$,且$f(4)=-\frac{7}{2}$,(1)求m的值;
(2)判断f(x)在(0,+∞)上的单调性,并给予证明.
分析 (1)根据$f(4)=-\frac{7}{2}$即可求出m=1;
(2)根据单调性定义,设任意的x1>x2>0,然后作差,通分,提取公因式,判断f(x1)与f(x2)的大小关系,从而得出f(x)的单调性.
解答 解:(1)$f(4)=\frac{2}{4}-{4}^{m}=-\frac{7}{2}$;
∴4m=4;
∴m=1;
(2)f(x)在(0,+∞)上单调递减.
理由:$f(x)=\frac{2}{x}-x$,设x1>x2>0,则:
$f({x}_{1})-f({x}_{2})=\frac{2}{{x}_{1}}-{x}_{1}-\frac{2}{{x}_{2}}+{x}_{2}$
=$\frac{2({x}_{2}-{x}_{1})}{{x}_{1}{x}_{2}}+({x}_{2}-{x}_{1})$
=$({x}_{2}-{x}_{1})(\frac{2}{{x}_{1}{x}_{2}}+1)$;
∵x1>x2>0;
∴x2-x1<0,$\frac{2}{{x}_{1}{x}_{2}}+1>0$;
∴f(x1)<f(x2);
∴f(x)在(0,+∞)上单调递减.
点评 考查已知函数求值,以及单调性定义,根据单调性定义判断一个函数单调性的方法和过程.

练习册系列答案
相关题目
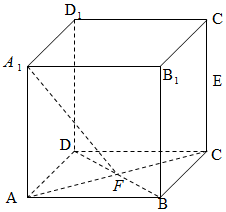 如图:已知在正方体ABCD-A1B1C1D1中,E是CC1的中点,F是AC,BD的交点.求A1F与B1E所成角的余弦值.
如图:已知在正方体ABCD-A1B1C1D1中,E是CC1的中点,F是AC,BD的交点.求A1F与B1E所成角的余弦值.