题目内容
8.在正六边形ABCDEF中,若$\overrightarrow{AB}$=$\overrightarrow{AC}$+λ$\overrightarrow{AD}$,则λ=-$\frac{1}{2}$.分析 根据向量加减运算的几何意义求出λ.
解答 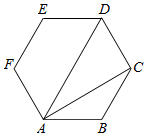 解由正六边形的知识可知$\overrightarrow{BC}=\frac{1}{2}$$\overrightarrow{AD}$,
解由正六边形的知识可知$\overrightarrow{BC}=\frac{1}{2}$$\overrightarrow{AD}$,
∵$\overrightarrow{AC}=\overrightarrow{AB}+\overrightarrow{BC}$=$\overrightarrow{AB}+\frac{1}{2}\overrightarrow{AD}$,
∴$\overrightarrow{AB}$=$\overrightarrow{AC}-\frac{1}{2}\overrightarrow{AD}$.
∴$λ=-\frac{1}{2}$
故答案为:$-\frac{1}{2}$.
点评 本题考查了平面向量的线性运算的几何意义,属于基础题.

练习册系列答案
相关题目
20.在△ABC中,A=60°,a=$\sqrt{6}$,b=$\sqrt{3}$,满足条件的△ABC ( )
| A. | 无解 | B. | 仅一解 | C. | 有两解 | D. | 不能确定 |
19.设集合M={-1,1},N={x|x2-x<6},则下列结论正确的是( )
| A. | N⊆M | B. | N∩M=∅ | C. | M⊆N | D. | M∩N=R |
13. 某校在一次高三年级“诊断性”测试后,对该年级的500名考生的成绩进行统计分析,成绩的频率分布表及频率分布直方图如图所示,规定成绩不小于125分为优秀.
某校在一次高三年级“诊断性”测试后,对该年级的500名考生的成绩进行统计分析,成绩的频率分布表及频率分布直方图如图所示,规定成绩不小于125分为优秀.
(1)若用分层抽样的方法从这500人中抽取4人的成绩进行分析,求其中成绩为优秀的学生人数;
(2)在(1)中抽取的4名学生中,随机抽取2名学生参加分析座谈会,求恰有1人成绩为优秀的概率.
 某校在一次高三年级“诊断性”测试后,对该年级的500名考生的成绩进行统计分析,成绩的频率分布表及频率分布直方图如图所示,规定成绩不小于125分为优秀.
某校在一次高三年级“诊断性”测试后,对该年级的500名考生的成绩进行统计分析,成绩的频率分布表及频率分布直方图如图所示,规定成绩不小于125分为优秀.(1)若用分层抽样的方法从这500人中抽取4人的成绩进行分析,求其中成绩为优秀的学生人数;
(2)在(1)中抽取的4名学生中,随机抽取2名学生参加分析座谈会,求恰有1人成绩为优秀的概率.
| 区间 | 人数 |
| [115,120) | 25 |
| [120,125) | a |
| [125,130) | 175 |
| [130,135) | 150 |
| [135,140) | b |
18.当a>1时,不等式${log_a}(4-x)>-{log_{\frac{1}{a}}}x$的解集是( )
| A. | (0,2) | B. | (0,4) | C. | (2,4) | D. | (0,+∞) |