题目内容
13. 某校在一次高三年级“诊断性”测试后,对该年级的500名考生的成绩进行统计分析,成绩的频率分布表及频率分布直方图如图所示,规定成绩不小于125分为优秀.
某校在一次高三年级“诊断性”测试后,对该年级的500名考生的成绩进行统计分析,成绩的频率分布表及频率分布直方图如图所示,规定成绩不小于125分为优秀.(1)若用分层抽样的方法从这500人中抽取4人的成绩进行分析,求其中成绩为优秀的学生人数;
(2)在(1)中抽取的4名学生中,随机抽取2名学生参加分析座谈会,求恰有1人成绩为优秀的概率.
| 区间 | 人数 |
| [115,120) | 25 |
| [120,125) | a |
| [125,130) | 175 |
| [130,135) | 150 |
| [135,140) | b |
分析 (1)根据频率分布直方图,求出a,b的值,再根据分层抽样的定义即可求出.
(2)成绩小于125的1人记为A,成绩为优秀的3人为a、b、c,用列举法得出从中随机抽取2人的基本事件数和所抽的恰有1人成绩为优秀的基本事件数,求出概率.
解答 解:(1)根据频率分布直方图,得;
b=0.02×5×500=50,a=0.04×5×500=100,
成绩不小于125分为优秀,
则成绩优秀的人数为175+150+50=375,
用分层抽样的方法从这500人中抽取4人的成绩进行分析,则成绩为优秀的学生人数$\frac{375}{500}$×4=3人,
(2)成绩小于125的1人记为A,成绩为优秀的3人为a、b、c;
从这4中随机抽取2人,基本事件有
Aa、Ab、Ac、ab、ac、bc,共6种,
恰有1人成绩为优秀的基本事件有Aa、Ab、Ac共3种;
它的概率为P=$\frac{3}{6}$=$\frac{1}{2}$.
点评 本题考查了频率分布直方图的应用问题,也考查了古典概率的应用问题,解题时应用列举法求出概率,是基础题.

练习册系列答案
 口算小状元口算速算天天练系列答案
口算小状元口算速算天天练系列答案 天天练口算系列答案
天天练口算系列答案
相关题目
3.已知集合M={x|0<x<2},N={x|x>1},则M∩(∁RN)=( )
| A. | (0,1] | B. | [0,1) | C. | (1,2) | D. | [1,2) |
4.已知P为椭圆$\frac{x^2}{25}+\frac{y^2}{16}=1$上的点,点M为圆${C_1}:{(x+3)^2}+{y^2}=1$上的动点,点N为圆C2:(x-3)2+y2=1上的动点,则|PM|+|PN|的最大值为( )
| A. | 8 | B. | 12 | C. | 16 | D. | 20 |
18.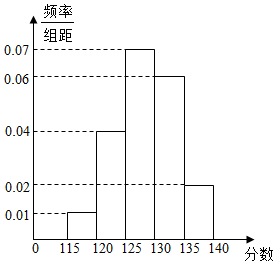 某校在一次高三年级“诊断性”测试后,对该年级的500名考生的成绩进行统计分析,成绩的频率分布表及频率分布直方图如图所示,规定成绩不小于125分为优秀.
某校在一次高三年级“诊断性”测试后,对该年级的500名考生的成绩进行统计分析,成绩的频率分布表及频率分布直方图如图所示,规定成绩不小于125分为优秀.
(1)若用分层抽样的方法从这500人中抽取20人的成绩进行分析,求其中成绩为优秀的学生人数;
(2)在(1)中抽取的20名学生中,要随机抽取2名学生参加分析座谈会,记其中成绩为优秀的人数为X,求X的分布列及数学期望.
 某校在一次高三年级“诊断性”测试后,对该年级的500名考生的成绩进行统计分析,成绩的频率分布表及频率分布直方图如图所示,规定成绩不小于125分为优秀.
某校在一次高三年级“诊断性”测试后,对该年级的500名考生的成绩进行统计分析,成绩的频率分布表及频率分布直方图如图所示,规定成绩不小于125分为优秀.(1)若用分层抽样的方法从这500人中抽取20人的成绩进行分析,求其中成绩为优秀的学生人数;
(2)在(1)中抽取的20名学生中,要随机抽取2名学生参加分析座谈会,记其中成绩为优秀的人数为X,求X的分布列及数学期望.
| 区间 | 人数 |
| [115,120) | 25 |
| [120,125) | a |
| [125,130) | 175 |
| [130,135) | 150 |
| [135,140) | b |
5.已知向量$\overrightarrow{a}$=(cosα,-2),$\overrightarrow{b}$=(sinα,1),且$\overrightarrow{a}$∥$\overrightarrow{b}$,则2snαcosα等于( )
| A. | -$\frac{4}{5}$ | B. | -3 | C. | 3 | D. | $\frac{4}{{5}_{\;}}$ |
2.某数学教师对所任教的两个班级各抽取20名学生进行测试,分数分布如表:
(Ⅰ)若成绩120分以上(含120分)为优秀,求从乙班参加测试的90分以上(含90分)的同学中,随机任取2名同学,恰有1人为优秀的概率;
(Ⅱ)根据以上数据完成下面的2×2列联表:在犯错概率小于0.1的前提下,你是否有足够的把握认为学生的数学成绩是否优秀与班级有关系?
${K^2}=\frac{{n{{({ad-bc})}^2}}}{{({a+b})({c+d})({a+c})({b+d})}}$,其中n=a+b+c+d.
| 分数区间 | 甲班频率 | 乙班频率 |
| [0,30) | 0.1 | 0.2 |
| [30,60) | 0.2 | 0.2 |
| [60,90) | 0.3 | 0.3 |
| [90,120) | 0.2 | 0.2 |
| [120,150) | 0.2 | 0.1 |
(Ⅱ)根据以上数据完成下面的2×2列联表:在犯错概率小于0.1的前提下,你是否有足够的把握认为学生的数学成绩是否优秀与班级有关系?
| 优秀 | 不优秀 | 总计 | |
| 甲班 | |||
| 乙班 | |||
| 总计 |
| k0 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
| P(K2≥k0) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |