题目内容
3．某工厂生产某种零件，已知日均销售量x（件）与货价P（元）之间的函数关系式为P=160-2x，生产x件成本的函数关系式为C=500+3x．试讨论，该工厂平均日销售量x为何值时，能获得最大利润？并求出最大利润？分析 根据利润=销售总额-成本总额，可得出利润=xP-C=x（160-2x）-（500+3x）=157x-2x2-500，利用二次函数的性质求出最大值即可．
解答 解：设该工厂平均日销售量为x，获得利润为y，
∴y=xP-C=x（160-2x）-（500+3x）=157x-2x2-500
=-2x2+157x-500，
对称轴x=$\frac{157}{4}$=39$\frac{1}{4}$，
显然当x=39时，有最大利润y=2581元
点评 考查了利用二次函数模型解决实际问题，属于基础题型，应熟练掌握．
练习册系列答案
灵星计算小达人系列答案
孟建平错题本系列答案
相关题目
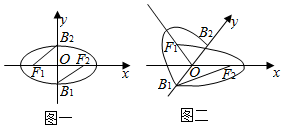
14．如图，椭圆$\frac{{x}^{2}}{3}$+y2=1的左、右焦点分别为F1，F2，短轴端点分别为B1，B2，现沿B1B2将椭圆折成120°角（图二），则异面直线F1B2与B1F2所成角的余弦值为（ ）
| A． | 0 | B． | $\frac{1}{3}$ | C． | $\frac{2}{3}$ | D． | -$\frac{1}{3}$ |
11．已知$tan（x+\frac{π}{4}）=2$，则sin2x=（ ）
| A． | $\frac{1}{10}$ | B． | $\frac{1}{5}$ | C． | $\frac{3}{5}$ | D． | $\frac{9}{10}$ |
18．集合M={x|lg（1-x）＜0}，集合N={x|-1≤x≤1}，则M∩N=（ ）
| A． | （0，1） | B． | [0，1） | C． | [-1，1] | D． | [-1，1） |
15．设$\frac{a-2i}{5+bi}$=1（a，b∈R，i为虚数单位），则|a+bi|的值为（ ）
| A． | 2$\sqrt{7}$ | B． | $\sqrt{29}$ | C． | 3$\sqrt{3}$ | D． | 5 |
12．函数f（x）=log3（x-1）的定义域是（ ）
| A． | （1，+∞） | B． | [1，+∞） | C． | {x∈R|x≠1} | D． | R |
13．已知集合A={x|x＜1}，B={x|x＞0}，则A∩B等于（ ）
| A． | （-∞，0） | B． | （0，1） | C． | （-∞，1） | D． | （0，+∞） |