题目内容
19．设集合M={-1，1}，N={x|x2-x＜6}，则下列结论正确的是（ ）| A． | N⊆M | B． | N∩M=∅ | C． | M⊆N | D． | M∩N=R |
分析 求出集合N，从而判断出M，N的关系即可．
解答 解：集合M={-1，1}，N={x|x2-x＜6}={x|-2＜x＜3}，
则M⊆N，
故选：C．
点评 本题考查了充分必要条件，考查集合的包含关系，是一道基础题．
练习册系列答案
相关题目
14．如图，椭圆$\frac{{x}^{2}}{3}$+y2=1的左、右焦点分别为F1，F2，短轴端点分别为B1，B2，现沿B1B2将椭圆折成120°角（图二），则异面直线F1B2与B1F2所成角的余弦值为（ ）
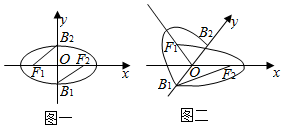
| A． | 0 | B． | $\frac{1}{3}$ | C． | $\frac{2}{3}$ | D． | -$\frac{1}{3}$ |
4．已知P为椭圆$\frac{x^2}{25}+\frac{y^2}{16}=1$上的点，点M为圆${C_1}：{（x+3）^2}+{y^2}=1$上的动点，点N为圆C2：（x-3）2+y2=1上的动点，则|PM|+|PN|的最大值为（ ）
| A． | 8 | B． | 12 | C． | 16 | D． | 20 |
11．已知$tan（x+\frac{π}{4}）=2$，则sin2x=（ ）
| A． | $\frac{1}{10}$ | B． | $\frac{1}{5}$ | C． | $\frac{3}{5}$ | D． | $\frac{9}{10}$ |
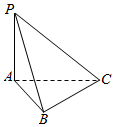如图，已知三棱锥P-ABC中，PA⊥面ABC，PA=3，AC=4，∠ABC=90°，AB=BC．