题目内容
15.阅读如图所示的程序框图,当输出的结果S为0时,判断框中应填( )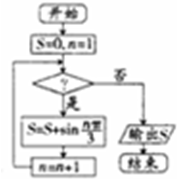
| A. | n≤4 | B. | n≤5 | C. | n≤7 | D. | n≤8 |
分析 模拟执行程序,可得当n=5时,满足判断框内的条件,当n=6时不满足判断框内的条件,退出循环,输出S的值为0,由此可得判断框内的条件.
解答 解:模拟程序的执行过程,可得
S=0,n=1
满足判断框内的条件,执行循环体,S=sin$\frac{π}{3}$,n=2
满足判断框内的条件,执行循环体,S=sin$\frac{π}{3}$+sin$\frac{2π}{3}$,n=3
满足判断框内的条件,执行循环体,S=sin$\frac{π}{3}$+sin$\frac{2π}{3}$+sinπ,n=4
满足判断框内的条件,执行循环体,S=sin$\frac{π}{3}$+sin$\frac{2π}{3}$+sinπ+sin$\frac{4π}{3}$,n=5
满足判断框内的条件,执行循环体,S=sin$\frac{π}{3}$+sin$\frac{2π}{3}$+sinπ+sin$\frac{4π}{3}$+sin$\frac{5π}{3}$=0,n=6
此时,由已知,应该不满足判断框内的条件,退出循环,输出S的值为0,
则判断框中的条件应该为:n≤5?
故选:B.
点评 本题考查的知识点是循环结构的程序框图的应用,根据程序输出S的值以及每次循环得到的n的值判断退出循环的条件是解题的关键,属于基础题.

练习册系列答案
 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案
相关题目
5.设双曲线$\frac{x^2}{a^2}$-$\frac{y^2}{b^2}$=1(a>0,b>0)的右焦点为F,过点F作x轴的垂线交两渐近线于点A,B两点,且与双曲线在第一象限的交点为P,设O为坐标原点,若$\overrightarrow{OP}$=λ$\overrightarrow{OA}$+u$\overrightarrow{OB}$(λ,μ∈R),λ2+u2=$\frac{5}{8}$,则双曲线的离心率为( )
| A. | $\frac{{2\sqrt{3}}}{3}$ | B. | $\frac{{3\sqrt{5}}}{5}$ | C. | $\frac{{3\sqrt{2}}}{2}$ | D. | $\frac{9}{8}$ |
3.在直二面角α-l-β中,线段AB的端点A,B分别在α,β内,且AB与α,β所成的角均为30°,则AB与l所成的角为( )
| A. | 30° | B. | 45° | C. | 60° | D. | 90° |
10. 某几何体的三视图如图所示,它的体积为( )
某几何体的三视图如图所示,它的体积为( )
 某几何体的三视图如图所示,它的体积为( )
某几何体的三视图如图所示,它的体积为( )| A. | π | B. | $\frac{4π}{3}$ | C. | $\frac{5π}{3}$ | D. | 2π |
4.cos$\frac{11}{4}$π的值为( )
| A. | $\frac{1}{2}$ | B. | -$\frac{1}{2}$ | C. | $\frac{\sqrt{2}}{2}$ | D. | -$\frac{\sqrt{2}}{2}$ |
5.甲、乙、丙三台机器是否需要维修相互之间没有影响,在一小时内甲、乙、丙三台机床需要维修的概率分别是0.1,0.2,0.4,则一小时内恰有一台机床需要维修的概率是( )
| A. | 0.444 | B. | 0.008 | C. | 0.7 | D. | 0.233 |
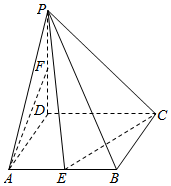 如图,在四棱锥P-ABCD中,底面ABCD为菱形,∠DAB=60°,PD⊥平面ABCD,PD=AD=2,点E,F分别为AB和PD的中点.
如图,在四棱锥P-ABCD中,底面ABCD为菱形,∠DAB=60°,PD⊥平面ABCD,PD=AD=2,点E,F分别为AB和PD的中点.