题目内容
3.已知两点A(-3,4),B(3,2),过点P(1,0)的直线l与线段AB有公共点,则直线l的斜率k的取值范围是( )| A. | (-1,1) | B. | (-∞,-1)∪(1,+∞) | C. | [-1,1] | D. | (-∞,-1]∪[1,+∞) |
分析 根据两点间的斜率公式,利用数形结合即可求出直线斜率的取值范围.
解答  解:∵点A(-3,4),B(3,2),过点P(1,0)的直线L与线段AB有公共点,
解:∵点A(-3,4),B(3,2),过点P(1,0)的直线L与线段AB有公共点,
∴直线l的斜率k≥kPB或k≤kPA,
∵PA的斜率为$\frac{4-0}{-3-1}$=-1,PB的斜率为$\frac{2-0}{3-1}$=1,
∴直线l的斜率k≥1或k≤-1,
故选:D
点评 本题主要考查直线的斜率的求法,利用数形结合是解决本题的关键,比较基础.

练习册系列答案
 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案
相关题目
18.户外运动已经成为一种时尚运动,某单位为了了解员工喜欢户外运动是否与性别有关,对本单位的50名员工进行了问卷调查,得到了如下联表:已知在这50人中随机抽取1人抽到喜欢户外运动的员工的概率是$\frac{3}{5}$
(1)请将列联表补充完整:
(2)是否有99%的把握认为喜欢户外运动与性别有关?并说明理由.下面临界值仅供参考:(大于2.706-90%,大于3.841-95%,大于6.635-99%)
(参考公式:K2=$\frac{{n(ad-bc)}^{2}}{(a+b)(c+d)(a+c)(b+d)}$,其中n=a+b+c+d)
| 喜欢户外活动 | 不喜欢户外活动 | 合计 | |
| 男性 | 20 | 5 | 25 |
| 女性 | 10 | 15 | 25 |
| 合计 | 30 | 20 | 50 |
(2)是否有99%的把握认为喜欢户外运动与性别有关?并说明理由.下面临界值仅供参考:(大于2.706-90%,大于3.841-95%,大于6.635-99%)
(参考公式:K2=$\frac{{n(ad-bc)}^{2}}{(a+b)(c+d)(a+c)(b+d)}$,其中n=a+b+c+d)
8.若三棱锥P-ABC中,AB=AC=1,AB⊥AC,PA⊥平面ABC,且直线PA与平面PBC所成角的正切值为$\frac{1}{2}$,则三棱锥P-ABC的外接球的表面积为( )
| A. | 4π | B. | 8π | C. | 16π | D. | 32π |
12.三个数0.76,60.7,log0.76的大小关系为( )
| A. | ${log_{0.7}}6<{0.7^6}<{6^{0.7}}$ | B. | 0.76<60.7<log0.76 | ||
| C. | ${log_{0.7}}6<{6^{0.7}}<{0.7^6}$ | D. | ${0.7^6}<{log_{0.7}}6<{6^{0.7}}$ |
13.下列判断错误的是( )
| A. | “若m>0,则方程x2+x-m=0有两个不同的实数根”是真命题. | |
| B. | 命题“若x2-3x+2=0,则x=1”的逆否命题为:“若x≠1,则x2-3x+2≠0”. | |
| C. | 若命题p:?x∈R,x2+x+1>0,则?p:?x∈R,x2+x+1≤0. | |
| D. | 若p∧q为假命题,则p,q均为假命题. |
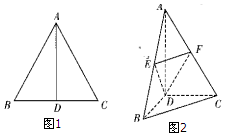 如图,边长为2的等边三角形ABC中,D为BC的中点,将△ABC沿AD翻折成直二面角B-AD-C,点E,F分别是AB,AC的中点.
如图,边长为2的等边三角形ABC中,D为BC的中点,将△ABC沿AD翻折成直二面角B-AD-C,点E,F分别是AB,AC的中点.