题目内容
设y=x2-ax+b,A={x|y-x=0},B={x|y-ax=0},若A={-3,1},试用列举法表示集合B.
考点:集合的表示法
专题:集合
分析:利用根与系数的关系可得a,b,再利用一元二次方程的解法即可得出集合B.
解答:
解:∵A={-3,1},∴-3,1是方程x=x2-ax+b的两个实数根,
∴
解得a=-3,b=-3.
因此x2-ax+b-ax=0可化为x2+6x-3=0.
∴x=
=-3±2
.
∴B={-3+2
,-3-2
}
∴
|
解得a=-3,b=-3.
因此x2-ax+b-ax=0可化为x2+6x-3=0.
∴x=
-6±4
| ||
| 2 |
| 3 |
∴B={-3+2
| 3 |
| 3 |
点评:本题查克拉一元二次方程的解法、集合的列举法,考查了计算能力,属于基础题.

练习册系列答案
相关题目
若f(x)=sinx+cos5,则该函数在点(5,f(5))处切线的斜率等于( )
| A、sin5+cos5 |
| B、cos5 |
| C、sin5 |
| D、sin5-cos5 |
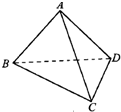 如图四面体ABCD的棱BD长为2,其余各棱长均为
如图四面体ABCD的棱BD长为2,其余各棱长均为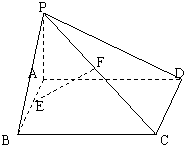 如图,已知矩形ABCD所在平面外一点P,PA⊥平面ABCD,E、F分别是AB,PC的中点.
如图,已知矩形ABCD所在平面外一点P,PA⊥平面ABCD,E、F分别是AB,PC的中点.