题目内容
求证：当a，b，c，d＞0．
（1）
≥
；
（2）
≥
．
（1）
| a+b+c |
| 3 |
| 3 | abc |
（2）
| a+b+c+d |
| 4 |
| 4 | abcd |
考点：不等式的证明
专题：不等式的解法及应用
分析：（1）由a，b，c＞0．可得a3+b3+c3-3abc=（a+b）3+c3-（3abc+3a2b+3ab2）=（a+b+c）（a2+b2+c2+2ab-ac-bc）-3ab（a+b+c）=（a+b+c）（a2+b2+c2-ab-ac-bc），再通过配方即可证明a3+b3+c3≥3abc，进而得到
≥
，当且仅当a=b=c时取等号．
（2）由a，b，c，d＞0，利用基本不等式可得a+b≥2
，c+d≥2
．再一次利用基本不等式即可证明．
| a+b+c |
| 3 |
| 3 | abc |
（2）由a，b，c，d＞0，利用基本不等式可得a+b≥2
| ab |
| cd |
解答：
证明：（1）∵a，b，c＞0．
∴a3+b3+c3-3abc=（a+b）3+c3-（3abc+3a2b+3ab2）=（a+b+c）（a2+b2+c2+2ab-ac-bc）-3ab（a+b+c）
=（a+b+c）（a2+b2+c2-ab-ac-bc）
=
(a+b+c)[(a-b)2+(b-c)2+(a-c)2]≥0．
∴a3+b3+c3≥3abc，
∴
≥
，当且仅当a=b=c时取等号．
（2）∵a，b，c，d＞0，∴a+b≥2
，c+d≥2
．
∴a+b+c+d≥2
+2
≥4
=4
，当且仅当a=b=c=d时取等号．
∴
≥
．
∴a3+b3+c3-3abc=（a+b）3+c3-（3abc+3a2b+3ab2）=（a+b+c）（a2+b2+c2+2ab-ac-bc）-3ab（a+b+c）
=（a+b+c）（a2+b2+c2-ab-ac-bc）
=
| 1 |
| 2 |
∴a3+b3+c3≥3abc，
∴
| a+b+c |
| 3 |
| 3 | abc |
（2）∵a，b，c，d＞0，∴a+b≥2
| ab |
| cd |
∴a+b+c+d≥2
| ab |
| cd |
|
| 4 | abcd |
∴
| a+b+c+d |
| 4 |
| 4 | abcd |
点评：本题考查了均值不等式的证明方法，考查了推理能力和计算能力，属于难题．
练习册系列答案
天天向上口算本系列答案
相关题目
对于推理：若a＞b，则a2＞b2，因为2＞-2，则22＞（-2）2，即4＞4，下列说法正确的是（ ）
| A、大前提错误 |
| B、小前提错误 |
| C、推理正确 |
| D、不是演绎推理 |
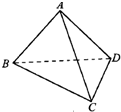如图四面体ABCD的棱BD长为2，其余各棱长均为