题目内容
12.若$x∈({e,{e^2}}),a=lnx,b={({\frac{1}{2}})^{lnx}},c={e^{lnx}}$,则a,b,c的大小关系为( )| A. | c>b>a | B. | c>a>b | C. | a>b>c | D. | b>c>a |
分析 x∈(e,e2),可得lnx∈(1,2),再利用指数函数与对数函数的单调性即可得出.
解答 解:∵x∈(e,e2),∴a=lnx∈(1,2),$b=(\frac{1}{2})^{lnx}$∈$(\frac{1}{4},\frac{1}{2})$,c=elnx∈(e,e2),
∴c>a>b.
故选:B.
点评 本题考查了指数函数与对数函数的单调性,考查了推理能力与计算能力,属于基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
4.设集合M={x|2x+1>1},N={x|lnx≤1},则M∩N等于( )
| A. | (-∞,e] | B. | (-1,1] | C. | (0,1) | D. | (0,e] |
2.用数学归纳法证明不等$\frac{1}{n+1}+\frac{1}{n+2}+…+\frac{1}{2n}>\frac{11}{24}({n∈{N^*}})$式的过程中,由n=k递推到n=k+1时,下列说法正确的是( )
| A. | 增加了一项$\frac{1}{{2({k+1})}}$ | B. | 增加了两项$\frac{1}{2k+1}$和$\frac{1}{{2({k+1})}}$ | ||
| C. | 增加了B中两项,但又少了一项$\frac{1}{k+1}$ | D. | 增加了A中一项,但又少了一项$\frac{1}{k+1}$ |
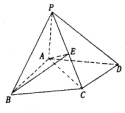 在四棱锥P-ABCD中,△ABC为正三角形,AB⊥AD,AC⊥CD,PA⊥平面ABCD,PC与平面ABCD所成角为45°
在四棱锥P-ABCD中,△ABC为正三角形,AB⊥AD,AC⊥CD,PA⊥平面ABCD,PC与平面ABCD所成角为45°