题目内容
20．已知直线l1：ax+4y-1=0，l2：x+ay-$\frac{1}{2}$=0，若l1∥l2，则实数a=-2．分析 利用直线平行的性质求解．
解答 解：∵直线l1：ax+4y-1=0，l2：x+ay-$\frac{1}{2}$=0，
∴$\frac{a}{1}=\frac{4}{a}≠\frac{-1}{-\frac{1}{2}}$，
解得a=-2（a=2时，两条直线重合，舍去）．
故答案为：-2．
点评 本题考查实数值的求法，是基础题，解题时要认真审题，注意直线平行的性质的灵活运用．
练习册系列答案
相关题目
11．已知命题q：?x∈R，cosx≤1，则￢q是（ ）
| A． | ?x∈R，cosx≥1 | B． | ?x∈R，cosx＞1 | C． | ?x0∈R，cosx0≥1 | D． | ?x0∈R，cosx0＞1 |
8．设m，n是两条不同的直线，α，β是两个不同的平面，下列说法正确的是（ ）
| A． | 若m∥α，α∩β=n，则 m∥n | B． | 若m∥α，m⊥n，则n⊥α | ||
| C． | 若m⊥α，n⊥α，则m∥n | D． | 若m?α，n?β，α⊥β，则m⊥n |
15．圆柱被一个平面截去一部分后与一个四棱锥组成的几何体的三视图如图所示，则该几何体的体积为（ ）
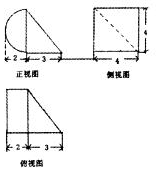
| A． | 4π+8 | B． | 8π+16 | C． | 16π+16 | D． | 16π+48 |
在直三棱柱ABC-A1B1C1中，D，E分别是BC，A1B1的中点．
12．若$x∈（{e，{e^2}}），a=lnx，b={（{\frac{1}{2}}）^{lnx}}，c={e^{lnx}}$，则a，b，c的大小关系为（ ）
| A． | c＞b＞a | B． | c＞a＞b | C． | a＞b＞c | D． | b＞c＞a |
随着经济模式的改变，微商和电商已成为当今城乡一种新型的购销平台．已知经销某种商品的电商在任何一个销售季度内，每售出1吨该商品可获利润0.5万元，未售出的商品，每1吨亏损0.3万元．根据往年的销售经验，得到一个销售季度内市场需求量的频率分布直方图如右图所示．已知电商为下一个销售季度筹备了130吨该商品．现以x（单位：吨，100≤x≤150）表示下一个销售季度的市场需求量，T（单位：万元）表示该电商下一个销售季度内经销该商品获得的利润．
10．若函数$f（x）={x^2}+ax+\frac{1}{x}$在$（{\frac{1}{2}\;\;，\;\;1}）$内任取两个实数p，q，且p≠q，不等式$\frac{f（p）-f（q）}{p-q}＞0$恒成立，则a的取值范围是（ ）
| A． | [-1，0] | B． | [-1，+∞） | C． | [0，3] | D． | [3，+∞） |