题目内容
14.若函数f(x)=2|x+a|满足f(3+x)=f(3-x),且f(x)在(-∞,m]上单调递减,则实数m的最大值等于( )| A. | -2 | B. | 1 | C. | 2 | D. | 3 |
分析 由题意可得函数f(x)关于x=3对称,可知f(x)又关于x=-a对称,求得a=-3,可知(-∞,m]⊆(-∞,3],即可得到m的最大值.
解答 解:函数f(x)=2|x+a|满足f(3+x)=f(3-x),
可得函数关于x=3对称,
又函数f(x)=2|x+a|关于x=-a对称,
则-a=3,可知a=-3,
f(x)=2|x-3|在(-∞,3]递减,
f(x)在(-∞,m]上单调递减,
可知(-∞,m]⊆(-∞,3],
即有m≤3,
则m的最大值为3.
故选:D.
点评 本题考查函数的性质和运用,主要是对称性和单调性的运用,考查化简和推理能力,属于中档题.

练习册系列答案
相关题目
5.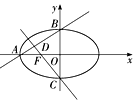 如图所示,椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率e=$\frac{1}{2}$,左焦点为F,A、B、C为其三个顶点,直线CF与AB交于D点,则tan∠ADF的值等于( )
如图所示,椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率e=$\frac{1}{2}$,左焦点为F,A、B、C为其三个顶点,直线CF与AB交于D点,则tan∠ADF的值等于( )
 如图所示,椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率e=$\frac{1}{2}$,左焦点为F,A、B、C为其三个顶点,直线CF与AB交于D点,则tan∠ADF的值等于( )
如图所示,椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率e=$\frac{1}{2}$,左焦点为F,A、B、C为其三个顶点,直线CF与AB交于D点,则tan∠ADF的值等于( )| A. | 3$\sqrt{3}$ | B. | -3$\sqrt{3}$ | C. | $\frac{\sqrt{3}}{5}$ | D. | -$\frac{\sqrt{3}}{5}$ |
19.执行如图所示的程序框图,如果输入a=-1,b=-3,则输出的a的值为( )


| A. | 27 | B. | 8 | C. | 9 | D. | 3 |
6.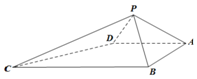 如图,四棱锥P-ABCD中,∠ABC=∠BAD=90°,BC=2AD,△PAB和△PAD都是等边三角形,则直线PC与平面ABCD所成角的正切值为( )
如图,四棱锥P-ABCD中,∠ABC=∠BAD=90°,BC=2AD,△PAB和△PAD都是等边三角形,则直线PC与平面ABCD所成角的正切值为( )
 如图,四棱锥P-ABCD中,∠ABC=∠BAD=90°,BC=2AD,△PAB和△PAD都是等边三角形,则直线PC与平面ABCD所成角的正切值为( )
如图,四棱锥P-ABCD中,∠ABC=∠BAD=90°,BC=2AD,△PAB和△PAD都是等边三角形,则直线PC与平面ABCD所成角的正切值为( )| A. | $\frac{{\sqrt{5}}}{5}$ | B. | $\sqrt{5}$ | C. | $\frac{{\sqrt{2}}}{2}$ | D. | $\sqrt{2}$ |
3.已知中心在原点的椭圆与双曲线有公共焦点,左,右焦点分别为F1,F2,且两条曲线在第一象限的交点为P,△PF1F2是以PF1为底边的等腰三角形,若|PF1|=8,椭圆与双曲线的离心率分别为e1,e2,则e1•e2+1的取值范围是( )
| A. | (1,+∞) | B. | $(\frac{8}{3},+∞)$ | C. | $(\frac{4}{3},+∞)$ | D. | $(\frac{10}{9},+∞)$ |
4.已知点A是抛物线$y=\frac{1}{4}{x^2}$的对称轴与准线的交点,点F为该抛物线的焦点,点P在抛物线上,且满足|PF|=m|PA|,当M取得最小值时,点P恰好在以A,F为焦点的双曲线上,则该双曲线的离心率为( )
| A. | $\frac{{\sqrt{5}+1}}{2}$ | B. | $\frac{{\sqrt{2}+1}}{2}$ | C. | $\sqrt{2}+1$ | D. | $\sqrt{5}+1$ |