题目内容
13.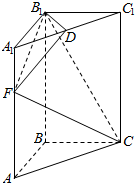 如图,高为3的直三棱柱ABC-A1B1C1中,底面是直角三角形,AC=2,D为A1C1的中点,F在线段AA1上,CF⊥DB1,且A1F=1.
如图,高为3的直三棱柱ABC-A1B1C1中,底面是直角三角形,AC=2,D为A1C1的中点,F在线段AA1上,CF⊥DB1,且A1F=1.(1)求证:CF⊥平面B1DF;
(2)求平面B1FC与平面AFC所成的锐二面角的余弦值.
分析 (1)根据线面垂直的判定定理先证明CF⊥B1F即即可证明CF⊥平面B1DF;
(2)根据二面角的定义先找出二面角的平面角即可求平面B1FC与平面AFC所成的锐二面角的余弦值.
解答 (1)证明:∵直三棱柱ABC-A1B1C1中,底面是直角三角形,D为A1C1的中点,
∴DB1⊥AA1,
∵CF⊥DB1,CF∩⊥AA1=F.
∴DB1⊥平面AA1CC1.
∴DB1⊥A1B1,
则△A1B1C1为等腰直角三角形,
∵直三棱柱ABC-A1B1C1中高为3,AC=2,A1F=1
∴AB=BC=$\sqrt{2}$,AF=2,FB1=$\sqrt{3}$,B1C=$\sqrt{11}$,CF=2$\sqrt{2}$,
满足B1F2+CF2=B1C2,
即CF⊥B1F,
∵CF⊥DB1,DB1∩B1F=B1,
∴CF⊥平面B1DF;
(2)∵CF⊥平面B1DF,B1F?平面B1DF,DF?平面B1DF,
∴CF⊥B1F,CF⊥DF,
∵DB1⊥平面AA1CC1.
∴∠B1FD是平面B1FC与平面AFC所成的锐二面角的平面角,
则B1D=1,DF=$\sqrt{2}$,
则cos∠B1FD=$\frac{DF}{{B}_{1}F}$=$\frac{\sqrt{2}}{\sqrt{3}}$=$\frac{\sqrt{6}}{3}$,
即平面B1FC与平面AFC所成的锐二面角的余弦值为$\frac{\sqrt{6}}{3}$.
点评 本题主要考查空间线面垂直的判断以及二面角的求解,利用线面垂直的判定定理以及二面角的定义是解决本题的关键.考查学生的运算和推理能力.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
4.在8件同类产品中,有5件正品,3件次品,从中任意抽取4件,下列事件中的必然事件是( )
| A. | 4件都是正品 | B. | 至少有一件次品 | C. | 4件都是次品 | D. | 至少有一件正品 |
19.点A(1,1)在直线l:mx+ny=1上,则mn的最大值为( )
| A. | $\frac{1}{8}$ | B. | $\frac{1}{4}$ | C. | $\frac{1}{2}$ | D. | 1 |
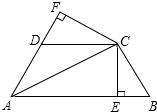 如图,已知AC平分∠BAD,CE⊥AB于点E,CF⊥AD于点F,且BC=CD.
如图,已知AC平分∠BAD,CE⊥AB于点E,CF⊥AD于点F,且BC=CD. 的夹角为60°,且
的夹角为60°,且 ,则
,则 ____________.
____________. 满足
满足 ,则
,则 ____________.
____________.