题目内容
如图,过点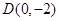 作抛物线
作抛物线 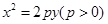 的切线
的切线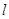 ,切点A在第二象限.
,切点A在第二象限.
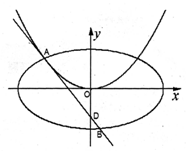
(1)求切点A的纵坐标;
(2)若离心率为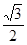 的椭圆
的椭圆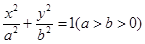 恰好经过切点A,设切线
恰好经过切点A,设切线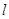 交椭圆的另一点为B,记切线
交椭圆的另一点为B,记切线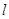 ,OA,OB的斜率分别为
,OA,OB的斜率分别为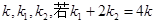 ,求椭圆方程.
,求椭圆方程.
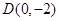 作抛物线
作抛物线 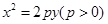 的切线
的切线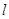 ,切点A在第二象限.
,切点A在第二象限.
(1)求切点A的纵坐标;
(2)若离心率为
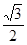 的椭圆
的椭圆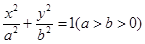 恰好经过切点A,设切线
恰好经过切点A,设切线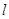 交椭圆的另一点为B,记切线
交椭圆的另一点为B,记切线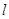 ,OA,OB的斜率分别为
,OA,OB的斜率分别为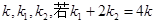 ,求椭圆方程.
,求椭圆方程.(Ⅰ) 
 (Ⅱ)
(Ⅱ) 

 (Ⅱ)
(Ⅱ) 
本试题主要是结合了导数的几何意义,得到直线的方程,以及运用设而不求的联立方程组的思想求解得到斜率的关系式,从而得到求解。
(1)利用导数的几何意义得到切点的横坐标,从而得到纵坐标。
(2)因为离心率为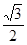 的椭圆
的椭圆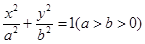 恰好经过切点A,设切线
恰好经过切点A,设切线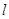 交椭圆的另一点为B,记切线
交椭圆的另一点为B,记切线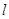 ,OA,OB的斜率分别为
,OA,OB的斜率分别为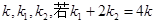 ,借助于韦达定理求解椭圆方程.
,借助于韦达定理求解椭圆方程.
解:(Ⅰ)设切点 ,且
,且 ,
,
由切线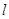 的斜率为
的斜率为 ,
,
得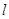 的方程为
的方程为 ,又点
,又点 在
在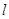 上,
上, ,即点
,即点 的纵坐标
的纵坐标
 .…………5分
.…………5分
(Ⅱ)由(Ⅰ) 得 ,切线斜率
,切线斜率 ,
,
设 ,切线方程为
,切线方程为 ,由
,由 ,得
,得 ,…………7分
,…………7分
所以椭圆方程为 ,且过
,且过 ,
, …………9分
…………9分
由 ,
,
 ,…………………11分
,…………………11分
∴

将 ,
, 代入得:
代入得: ,所以
,所以 ,
,
∴椭圆方程为 .………………13分
.………………13分
OB的斜率分别为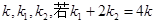 ,求椭圆方程.
,求椭圆方程.
(1)利用导数的几何意义得到切点的横坐标,从而得到纵坐标。
(2)因为离心率为
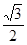 的椭圆
的椭圆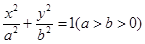 恰好经过切点A,设切线
恰好经过切点A,设切线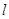 交椭圆的另一点为B,记切线
交椭圆的另一点为B,记切线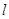 ,OA,OB的斜率分别为
,OA,OB的斜率分别为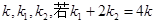 ,借助于韦达定理求解椭圆方程.
,借助于韦达定理求解椭圆方程.解:(Ⅰ)设切点
 ,且
,且 ,
,由切线
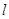 的斜率为
的斜率为 ,
,得
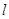 的方程为
的方程为 ,又点
,又点 在
在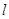 上,
上, ,即点
,即点 的纵坐标
的纵坐标
 .…………5分
.…………5分(Ⅱ)由(Ⅰ) 得
 ,切线斜率
,切线斜率 ,
,设
 ,切线方程为
,切线方程为 ,由
,由 ,得
,得 ,…………7分
,…………7分所以椭圆方程为
 ,且过
,且过 ,
, …………9分
…………9分由
 ,
, ,…………………11分
,…………………11分∴


将
 ,
, 代入得:
代入得: ,所以
,所以 ,
,∴椭圆方程为
 .………………13分
.………………13分OB的斜率分别为
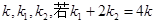 ,求椭圆方程.
,求椭圆方程.
练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
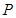 为圆
为圆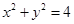 上的动点,且
上的动点,且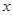 轴上,
轴上,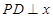 轴,垂足为
轴,垂足为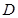 ,线段
,线段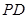 中点
中点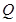 的轨迹为曲线
的轨迹为曲线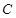 ,过定点
,过定点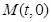
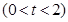 任作一条与
任作一条与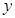 轴不垂直的直线
轴不垂直的直线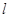 ,它与曲线
,它与曲线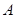 、
、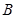 两点。
两点。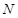 ,使得
,使得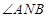 总能被
总能被 过点
过点 ,离心率为
,离心率为 ,⊙O的圆心在原点,直径为椭圆的短轴,⊙M的方程为
,⊙O的圆心在原点,直径为椭圆的短轴,⊙M的方程为 ,过⊙M上任一点P作⊙O的切线PA、PB,切点为A、B.
,过⊙M上任一点P作⊙O的切线PA、PB,切点为A、B.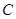 与椭圆
与椭圆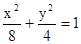 有相同的焦点,直线
有相同的焦点,直线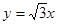 为
为 的离心率
的离心率 右焦点到直线
右焦点到直线 的距离
的距离 ,
, 为坐标原点。
为坐标原点。
 的方程;
的方程; 两点,证明点
两点,证明点 的距离为定值,并求弦
的距离为定值,并求弦 分别为椭圆
分别为椭圆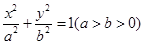 的左、右顶点,若在椭圆上存在异于
的左、右顶点,若在椭圆上存在异于 ,使得
,使得 ,其中
,其中 为坐标原点,则椭圆的离心率
为坐标原点,则椭圆的离心率 的取值范围是
的取值范围是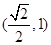


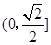
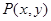 为动点,已知点
为动点,已知点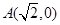 ,
,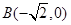 ,直线
,直线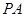 与
与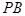 的斜率之积为
的斜率之积为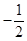 .
.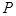 轨迹
轨迹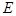 的方程;
的方程;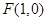 的直线
的直线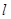 交曲线
交曲线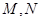 两点,设点
两点,设点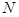 关于
关于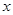 轴的对称点为
轴的对称点为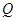 (
(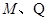 不重合),求证:直线
不重合),求证:直线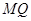 过定点.
过定点. 的离心率为
的离心率为 ,点
,点 ,
,  为
为 上两点,斜率为
上两点,斜率为 的直线与椭圆
的直线与椭圆 交于点
交于点 ,
, (
( 两侧).
两侧).
 面积的最大值;
面积的最大值; ,
, 的斜率为
的斜率为 ,试判断
,试判断 是否为定值.若是,求出这个定值;若不是,说明理由.
是否为定值.若是,求出这个定值;若不是,说明理由. 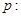 “椭圆
“椭圆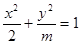 的焦点在
的焦点在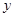 轴上”;
轴上”;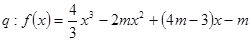 在
在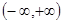 上单调递增,若“
上单调递增,若“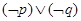 ”为假,求
”为假,求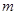 的取值范围.
的取值范围.