题目内容
(本题满分15分)设椭圆 的离心率
的离心率 右焦点到直线
右焦点到直线 的距离
的距离 ,
, 为坐标原点。
为坐标原点。

(Ⅰ)求椭圆 的方程;
的方程;
(Ⅱ)过点 作两条互相垂直的射线,与椭圆
作两条互相垂直的射线,与椭圆 分别交于
分别交于 两点,证明点
两点,证明点 到直线
到直线 的距离为定值,并求弦
的距离为定值,并求弦 长度的最小值.
长度的最小值.
 的离心率
的离心率 右焦点到直线
右焦点到直线 的距离
的距离 ,
, 为坐标原点。
为坐标原点。
(Ⅰ)求椭圆
 的方程;
的方程;(Ⅱ)过点
 作两条互相垂直的射线,与椭圆
作两条互相垂直的射线,与椭圆 分别交于
分别交于 两点,证明点
两点,证明点 到直线
到直线 的距离为定值,并求弦
的距离为定值,并求弦 长度的最小值.
长度的最小值.(Ⅰ) ;(Ⅱ)弦AB的长度的最小值是
;(Ⅱ)弦AB的长度的最小值是
 ;(Ⅱ)弦AB的长度的最小值是
;(Ⅱ)弦AB的长度的最小值是
本试题主要是考查了直线与椭圆的位置关系的运用以及椭圆方程的求解,韦达定理的综合运用。
(1)运用椭圆几何性质和点到直线的距离公式可知,a,b,c的关系式得到椭圆的方程。
(2)设出直线与椭圆联立方程组,然后借助于韦达定理和点到直线的距离,表示 ,然后利用
,然后利用 ,得到弦AB的长度的最小值是
,得到弦AB的长度的最小值是
解:(Ⅰ)由 , ………2分
, ………2分
由右焦点到直线 的距离
的距离 得:
得: ………5分
………5分
所以椭圆C的方程为 ……..6分
……..6分
(Ⅱ)设 当直线AB的斜率存在时,设为
当直线AB的斜率存在时,设为 ,与椭圆
,与椭圆
 联立消去
联立消去 得:
得:
由△>0得 ,
, 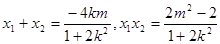 ………8分
………8分
 ,
, ,即
,即
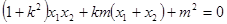

整理得 ………10分
………10分
所以O到直线AB的距离 ………12
………12
当直线AB的斜率不存在时易得 ,即命题得证;………13分
,即命题得证;………13分
又
由 ,
,
即弦AB的长度的最小值是 ………15分
………15分
(1)运用椭圆几何性质和点到直线的距离公式可知,a,b,c的关系式得到椭圆的方程。
(2)设出直线与椭圆联立方程组,然后借助于韦达定理和点到直线的距离,表示
 ,然后利用
,然后利用 ,得到弦AB的长度的最小值是
,得到弦AB的长度的最小值是
解:(Ⅰ)由
 , ………2分
, ………2分由右焦点到直线
 的距离
的距离 得:
得: ………5分
………5分所以椭圆C的方程为
 ……..6分
……..6分(Ⅱ)设
 当直线AB的斜率存在时,设为
当直线AB的斜率存在时,设为 ,与椭圆
,与椭圆
 联立消去
联立消去 得:
得:
由△>0得
 ,
, 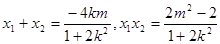 ………8分
………8分 ,
, ,即
,即
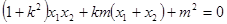

整理得
 ………10分
………10分所以O到直线AB的距离
 ………12
………12当直线AB的斜率不存在时易得
 ,即命题得证;………13分
,即命题得证;………13分又

由
 ,
,即弦AB的长度的最小值是
 ………15分
………15分
练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
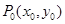 在椭圆
在椭圆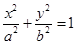 (
(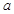 >0,
>0,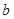 >0)外 ,则过
>0)外 ,则过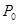 作椭圆的两条切线的切点为P1、P2,切点弦P1P2的直线方程是
作椭圆的两条切线的切点为P1、P2,切点弦P1P2的直线方程是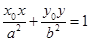 ,那么类比双曲线则有如下命题: 若
,那么类比双曲线则有如下命题: 若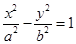 (
(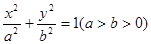 的左焦点
的左焦点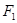 作
作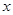 轴的垂线交椭圆于点
轴的垂线交椭圆于点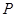 ,
,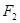 为右焦点,若
为右焦点,若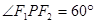 ,则椭圆的离心率为__________________ .
,则椭圆的离心率为__________________ .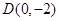 作抛物线
作抛物线 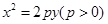 的切线
的切线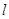 ,切点A在第二象限.
,切点A在第二象限.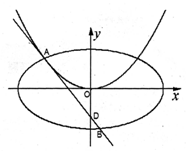
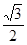 的椭圆
的椭圆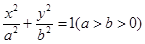 恰好经过切点A,设切线
恰好经过切点A,设切线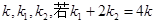 ,求椭圆方程.
,求椭圆方程. ,焦点在
,焦点在 轴上,离心率为
轴上,离心率为 ,且椭圆E上一点到两个焦点距离之和为4;
,且椭圆E上一点到两个焦点距离之和为4; ,
, 是过点
是过点 且相互垂直的两条直线,
且相互垂直的两条直线, ,
, 两点,
两点, ,
, 两点,
两点, ,
, 的中点分别为
的中点分别为 ,
, .
. 的取值范围;
的取值范围; 与直线
与直线 的斜率乘积为定值.
的斜率乘积为定值.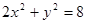 的长轴长是( )
的长轴长是( )
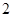


 的准线与
的准线与 轴交于
轴交于 ,焦点为
,焦点为 ,以
,以 的椭圆的两条准线之间的距离为 ( )
的椭圆的两条准线之间的距离为 ( ) 的离心率为( )
的离心率为( )



 的左、右焦点分别为
的左、右焦点分别为 ,若椭圆上存在点
,若椭圆上存在点 (异于长轴的端点),使得
(异于长轴的端点),使得 ,则该椭圆离心率的取值范围是 .
,则该椭圆离心率的取值范围是 .