题目内容
(本小题满分12分)
已知点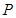 为圆
为圆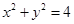 上的动点,且
上的动点,且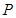 不在
不在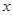 轴上,
轴上,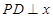 轴,垂足为
轴,垂足为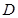 ,线段
,线段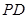 中点
中点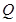 的轨迹为曲线
的轨迹为曲线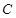 ,过定点
,过定点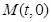
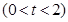 任作一条与
任作一条与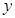 轴不垂直的直线
轴不垂直的直线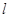 ,它与曲线
,它与曲线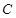 交于
交于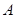 、
、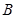 两点。
两点。
(I)求曲线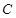 的方程;
的方程;
(II)试证明:在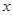 轴上存在定点
轴上存在定点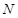 ,使得
,使得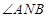 总能被
总能被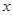 轴平分
轴平分
已知点
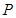 为圆
为圆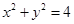 上的动点,且
上的动点,且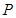 不在
不在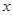 轴上,
轴上,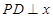 轴,垂足为
轴,垂足为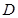 ,线段
,线段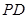 中点
中点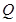 的轨迹为曲线
的轨迹为曲线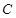 ,过定点
,过定点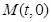
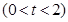 任作一条与
任作一条与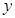 轴不垂直的直线
轴不垂直的直线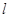 ,它与曲线
,它与曲线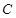 交于
交于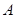 、
、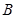 两点。
两点。(I)求曲线
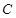 的方程;
的方程;(II)试证明:在
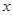 轴上存在定点
轴上存在定点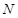 ,使得
,使得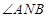 总能被
总能被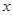 轴平分
轴平分(1) ;(2)见解析.
;(2)见解析.
 ;(2)见解析.
;(2)见解析.(Ⅰ)利用相关点法把所求点的问题转化已知动点问题,从而得到曲线的轨迹方程;(Ⅱ)联立方程,利用韦达定理及条件转化为点的坐标关系,从而求出点的坐标。
解:(1)设 为曲线
为曲线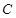 上的任意一点,则点
上的任意一点,则点 在圆
在圆 上,
上,
∴ ,曲线
,曲线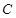 的方程为
的方程为 . ………………2分
. ………………2分
(2)设点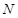 的坐标为
的坐标为 ,直线
,直线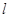 的方程为
的方程为 , ………………3分
, ………………3分
代入曲线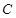 的方程
的方程 ,可得
,可得  ,……5分
,……5分
∵ ,∴
,∴ ,
,
∴直线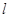 与曲线
与曲线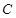 总有两个公共点.(也可根据点M在椭圆
总有两个公共点.(也可根据点M在椭圆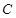 的内部得到此结论)
的内部得到此结论)
………………6分
设点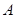 ,
,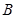 的坐标分别
的坐标分别 ,
,  ,则
,则 ,
,
要使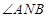 被
被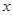 轴平分,只要
轴平分,只要 , ………………9分
, ………………9分
即 ,
, , ………………10分
, ………………10分
也就是 ,
, ,
,
即 ,即只要
,即只要 ………………12分
………………12分
当 时,(*)对任意的s都成立,从而
时,(*)对任意的s都成立,从而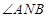 总能被
总能被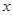 轴平分.
轴平分.
所以在x轴上存在定点 ,使得
,使得 总能被
总能被 轴平分.
轴平分.
解:(1)设
 为曲线
为曲线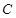 上的任意一点,则点
上的任意一点,则点 在圆
在圆 上,
上,∴
 ,曲线
,曲线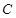 的方程为
的方程为 . ………………2分
. ………………2分 (2)设点
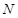 的坐标为
的坐标为 ,直线
,直线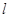 的方程为
的方程为 , ………………3分
, ………………3分 代入曲线
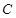 的方程
的方程 ,可得
,可得  ,……5分
,……5分 ∵
 ,∴
,∴ ,
,∴直线
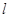 与曲线
与曲线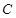 总有两个公共点.(也可根据点M在椭圆
总有两个公共点.(也可根据点M在椭圆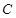 的内部得到此结论)
的内部得到此结论)………………6分
设点
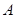 ,
,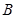 的坐标分别
的坐标分别 ,
,  ,则
,则 ,
, 要使
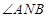 被
被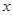 轴平分,只要
轴平分,只要 , ………………9分
, ………………9分即
 ,
, , ………………10分
, ………………10分也就是
 ,
, ,
, 即
 ,即只要
,即只要 ………………12分
………………12分 当
 时,(*)对任意的s都成立,从而
时,(*)对任意的s都成立,从而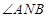 总能被
总能被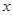 轴平分.
轴平分.所以在x轴上存在定点
 ,使得
,使得 总能被
总能被 轴平分.
轴平分.
练习册系列答案
相关题目
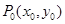 在椭圆
在椭圆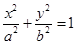 (
(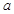 >0,
>0,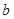 >0)外 ,则过
>0)外 ,则过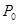 作椭圆的两条切线的切点为P1、P2,切点弦P1P2的直线方程是
作椭圆的两条切线的切点为P1、P2,切点弦P1P2的直线方程是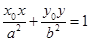 ,那么类比双曲线则有如下命题: 若
,那么类比双曲线则有如下命题: 若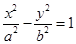 (
(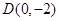 作抛物线
作抛物线 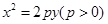 的切线
的切线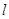 ,切点A在第二象限.
,切点A在第二象限.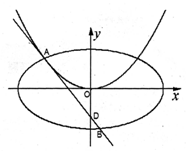
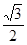 的椭圆
的椭圆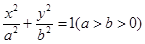 恰好经过切点A,设切线
恰好经过切点A,设切线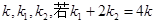 ,求椭圆方程.
,求椭圆方程. ,焦点在
,焦点在 轴上,离心率为
轴上,离心率为 ,且椭圆E上一点到两个焦点距离之和为4;
,且椭圆E上一点到两个焦点距离之和为4; ,
, 是过点
是过点 且相互垂直的两条直线,
且相互垂直的两条直线, ,
, 两点,
两点, ,
, 两点,
两点, ,
, 的中点分别为
的中点分别为 ,
, .
. 的取值范围;
的取值范围; 与直线
与直线 的斜率乘积为定值.
的斜率乘积为定值. +
+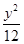 =1
=1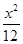 +
+ =1
=1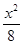 +
+ =1
=1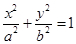 (a>b>0)的离心率
(a>b>0)的离心率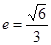 ,过点A(0,-b)和B(a,0)的直线与原点的距离为
,过点A(0,-b)和B(a,0)的直线与原点的距离为
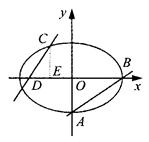
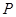 是椭圆
是椭圆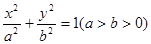 上一点,
上一点,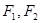 分别是椭圆的左、右焦点,
分别是椭圆的左、右焦点,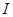 为
为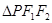 的内心,若
的内心,若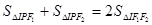 ,则该椭圆的离心率是( )
,则该椭圆的离心率是( )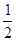



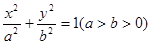 的左、右焦点分别为
的左、右焦点分别为 ,线段
,线段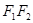 被抛物线
被抛物线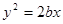 的焦点F分成5:3两段,则椭圆的离心率为 ( )
的焦点F分成5:3两段,则椭圆的离心率为 ( )



 的左、右焦点分别为
的左、右焦点分别为 ,若椭圆上存在点
,若椭圆上存在点 (异于长轴的端点),使得
(异于长轴的端点),使得 ,则该椭圆离心率的取值范围是 .
,则该椭圆离心率的取值范围是 .