题目内容
11．已知函数f（x）=|x-3|+|x+1|．（1）作出y=f（x）的图象；
（2）解不等式f（x）≤6．
分析 （1）将f（x）的绝对值去掉，写成分段函数的形式，由分段函数的图象即可得到所求图象；
（2）作出直线y=6，求得交点，由图象，即可得到所求解集．
解答 
解：（1）f（x）=$\left\{\begin{array}{l}{2-2x，x≤-1}\\{4，-1＜x＜3}\\{2x-2，x≥3}\end{array}\right.$，
作出函数f（x）的图象，如右：
（2）作出直线y=6，由|x-3|+|x+1|=6，
可得x=4或-2，
由图象可得f（x）≤6的解集为[-2，4]．
点评 本题考查绝对值函数的图象和运用，注意化为分段函数，考查数形结合的思想方法，属于基础题．
练习册系列答案
阅读快车系列答案
相关题目
6．
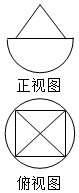一个半球与一个正四棱锥组成的几何体的正视图与俯视图如图所示，其中正视图中的等腰三角形的腰长为$\sqrt{3}$．若正四棱锥的顶点均在该半球所在球的球面上，则此球的半径为（ ）
一个半球与一个正四棱锥组成的几何体的正视图与俯视图如图所示，其中正视图中的等腰三角形的腰长为$\sqrt{3}$．若正四棱锥的顶点均在该半球所在球的球面上，则此球的半径为（ ）| A． | 2 | B． | $\frac{3}{2}$$\sqrt{2}$ | C． | $\frac{12}{5}$$\sqrt{5}$ | D． | $\sqrt{6}$ |