题目内容
16.已知函数f(x)的定义域为(0,+∞),且满足f(4)=1,对任意x1、x2∈(0,+∞)都有f(x1•x2)=f(x1)+f(x2),当x∈(0,1)时,f(x)<0.(1)证明函数f(x)在(0,+∞)上是增函数;
(2)解不等式f(3x+1)+f(2x-6)≤3.
分析 (1)由f(x1•x2)=f(x1)+f(x2),可得f(x1)-f(x2)=f($\frac{{x}_{1}}{{x}_{2}}$),结合x∈(0,1)时,f(x)<0.及增函数的定义可证得结论;
(2)令x1=x2=4,可得f(16)=2,x1=4,x2=16,可得f(64)=3,结合f(x)的定义域为(0,+∞),f(x1•x2)=f(x1)+f(x2),及(2)中函数的单调性,可将不等式f(3x+1)+f(2x-6)≤3转化为一个关于x的不等式组.本题考查的知识点是抽象函数及其应用.
解答 (1)证明:设x1,x2∈(0,+∞)且x1<x2,
∵对任意x1,x2(0,+∞),都有f(x1•x2)=f(x1)+f(x2),
∴f(x1)-f(x2)=f($\frac{{x}_{1}}{{x}_{2}}$)
∵0<x1<x2,
∴0<$\frac{{x}_{1}}{{x}_{2}}$<1,又当x∈(0,1)时,f(x)<0,∴f(x1)-f(x2)=f($\frac{{x}_{1}}{{x}_{2}}$)<0,
∴f(x)在(0,+∞)上是增函数(6分)
(2)解:令x1=x2=4,则f(16)=f(4)+f(4)=2,
令x1=4,x2=16,则f(64)=f(4)+f(16)=3,(8分)
∴f(3x+1)+f(2x-6)≤3=f(64)
结合f(x)的定义域为(0,+∞),f(x1•x2)=f(x1)+f(x2)恒成立
∴$\left\{\begin{array}{l}{3x+1>0}\\{2x-6>0}\\{(3x+1)(2x-6)≤64}\end{array}\right.$
∴x∈(3,5](12分)
点评 本题考查的是抽象函数及其应用,函数的单调性证明,以及赋值法的应用,属于中档题,在解答的过程当中充分体现了函数单调性的定义、作差法以及赋值法等知识.值得同学们体会和反思.

| A. | 上升1m | B. | 下降1m | C. | 上升2m | D. | 上升3m |
| A. | $\frac{17}{96}$ | B. | $\frac{5}{32}$ | C. | $\frac{7}{48}$ | D. | $\frac{1}{6}$ |
| A. | {x|0<x<2} | B. | {x|1<x<2} | C. | {x|0<x<1} | D. | {x|x<1} |
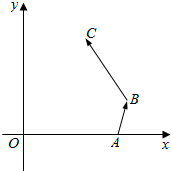 如图,在平面直角坐标系中,|$\overrightarrow{OA}$|=2|$\overrightarrow{AB}$|=2,∠OAB=$\frac{2π}{3}$,$\overrightarrow{BC}$=(-1,$\sqrt{3}$).
如图,在平面直角坐标系中,|$\overrightarrow{OA}$|=2|$\overrightarrow{AB}$|=2,∠OAB=$\frac{2π}{3}$,$\overrightarrow{BC}$=(-1,$\sqrt{3}$).