题目内容

6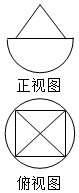．一个半球与一个正四棱锥组成的几何体的正视图与俯视图如图所示，其中正视图中的等腰三角形的腰长为$\sqrt{3}$．若正四棱锥的顶点均在该半球所在球的球面上，则此球的半径为（　　）
A．2B．$\frac{3}{2}$$\sqrt{2}$C．$\frac{12}{5}$$\sqrt{5}$D．$\sqrt{6}$

分析 利用正视图中的等腰三角形的腰长为$\sqrt{3}$，结合勾股定理，即可得出结论．

解答 解：由题意，设球的半径为r，则3=r2+（$\frac{1}{2}$r）2，
∴r=$\frac{12}{5}\sqrt{5}$．
故选：C．

点评 本题考查三视图，考查勾股定理，正确转化是关键．

练习册系列答案
相关题目
16．已知命题p：方程$\frac{x^2}{m+1}+\frac{y^2}{3-m}=1$表示焦点在y轴上的椭圆，命题q：关于x的方程x2+2mx+2m+3=0无实根，
（1）若命题p为真命题，求实数m的取值范围；
（2）若“p∧q”为假命题，“p∨q”为真命题，求实数m的取值范围．
17．已知（ω+x）6=a0+a1x+a2x2+…+a6x6，其中ω=-$\frac{1}{2}$+$\frac{\sqrt{3}}{2}$$\overrightarrow{i}$，则|a0|+|a1|+…+|a6|等于（　　）
A．1B．26C．$\frac{{2}^{6}+1}{2}$D．$\frac{{2}^{6}-1}{2}$
14．若函数f（x）的定义域为集合A，且函数f（x-1）的定义域是[5，17]．
（Ⅰ）求集合A；
（Ⅱ）设函数h（x）=（log2x）2-alog${\;}_{\sqrt{2}}$x+5（x∈A），求函数h（x）的最大值g（a）．
1．下列函数，在其定义域内，既是奇函数又是增函数的是（　　）
A．y=x${\;}^{\frac{1}{2}}$B．y=2xC．y=x3D．y=log2x
11．已知函数f（x）=|x-3|+|x+1|．
（1）作出y=f（x）的图象；
（2）解不等式f（x）≤6．
18．在平面直角坐标系中，方程|x|+|y|=4所表示的曲线是以（0，4），（4，0），（0，-4），（-4，0）为顶点的正方形．
15．已知$\overrightarrow{a}$=（3，1），$\overrightarrow{b}$=（1，2），则向量$\overrightarrow{a}$与$\overrightarrow{b}$的夹角为（　　）
A．$\frac{π}{6}$B．$\frac{π}{4}$C．$\frac{π}{3}$D．$\frac{π}{2}$
13．函数$f（x）=\sqrt{3x-{x^2}}$的定义域为（　　）
A．[-3，0]B．（-∞，-3]∪[0，+∞）C．[0，3]D．（-∞，0]∪[3，+∞）

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网