题目内容
设函数y=x2-3×2n-1x+2×4n-1(n∈N*)的图象在x轴上截得的线段长为dn,记数列{dn}的前n项和为Sn,若存在正整数n,使得log2(Sn+1) m-n2≥60成立,则实数m的最小值为 .
考点:数列的求和
专题:等差数列与等比数列
分析:令y=x2-3×2n-1x+2×4n-1=0,可得dn=x2-x1=2n-1.利用等比数列的前n项和公式可得Sn=2n-1.log2(Sn+1) m-n2≥60化为n(m-n2)≥60,
m≥
+n2,变形利用基本不等式的性质即可得出.
m≥
| 60 |
| n |
解答:
解:令y=x2-3×2n-1x+2×4n-1=0,解得x1=2n-1,x2=2×2n-1,
∴dn=x2-x1=2n-1.
∴Sn=
=2n-1.
∴log2(Sn+1) m-n2≥60化为n(m-n2)≥60,
∴m≥
+n2=
+
+n2≥3
=90,
取n=3时,m取得最小值29.
故答案为:29.
∴dn=x2-x1=2n-1.
∴Sn=
| 2n-1 |
| 2-1 |
∴log2(Sn+1) m-n2≥60化为n(m-n2)≥60,
∴m≥
| 60 |
| n |
| 30 |
| n |
| 30 |
| n |
| 3 |
| ||||
取n=3时,m取得最小值29.
故答案为:29.
点评:本题考查了等比数列的前n项和公式、基本不等式的性质、一元二次方程的解法,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案
相关题目
 某市司法部门为了宣传《宪法》举办法律知识问答活动,随机对该市18~68岁的人群抽取一个容量为n的样本,并将样本数据分成五组:[18,28),[28,38),[38,48),[48,58),[58,68),再将其按从左到右的顺序分别编号为第1组,第2组,…,第5组,绘制了样本的频率分布直方图;并对回答问题情况进行统计后,结果如下表所示.
某市司法部门为了宣传《宪法》举办法律知识问答活动,随机对该市18~68岁的人群抽取一个容量为n的样本,并将样本数据分成五组:[18,28),[28,38),[38,48),[48,58),[58,68),再将其按从左到右的顺序分别编号为第1组,第2组,…,第5组,绘制了样本的频率分布直方图;并对回答问题情况进行统计后,结果如下表所示.
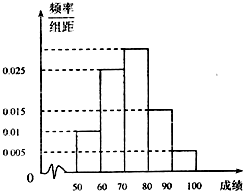 国家教育部要求高中阶段每学年都要组织学生进行“国家学生体质健康数据测试”,方案要求以学校为单位组织实施,某校对高一1班同学按照“国家学生体质健康数据测试”项目按百分制进行了测试,并对50分以上的成绩进行统计,其频率分布直方图如图所示,若90~100分数段的人数为2人.
国家教育部要求高中阶段每学年都要组织学生进行“国家学生体质健康数据测试”,方案要求以学校为单位组织实施,某校对高一1班同学按照“国家学生体质健康数据测试”项目按百分制进行了测试,并对50分以上的成绩进行统计,其频率分布直方图如图所示,若90~100分数段的人数为2人.