题目内容
5.已知复数z满足(1+i)•z=2-i,则复数z的共轭复数为( )| A. | $\frac{1}{2}-\frac{3}{2}i$ | B. | $\frac{1}{2}+\frac{3}{2}i$ | C. | 1+3i | D. | 1-3i |
分析 利用复数的运算法则、共轭复数的定义即可得出.
解答 解:∵(1+i)•z=2-i,∴(1-i)(1+i)•z=(1-i)(2-i),
∴2z=1-3i,∴z=$\frac{1}{2}$-$\frac{3}{2}$i.
则复数z的共轭复数为$\frac{1}{2}$+$\frac{3}{2}$i.
故选:B.
点评 本题考查了复数的运算法则、共轭复数的定义,考查了推理能力与计算能力,属于基础题.

练习册系列答案
 习题精选系列答案
习题精选系列答案
相关题目
10.如图所示,向量$\overrightarrow{O{Z_1}},\overrightarrow{O{Z_2}}$所对应的复数分别为Z1,Z2,则Z1•Z2=( )
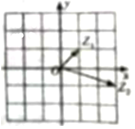

| A. | 4+2i | B. | 2+i | C. | 2+2i | D. | 3+i |
17.将函数$f(x)=3sin(2x+\frac{π}{3})$的图象向左平移$\frac{π}{6}$个单位,在向上平移1个单位,得到g(x)的图象,若g(x1)g(2)=16,且${x_1},{x_2}∈[-\frac{3π}{2},\frac{3π}{2}]$,则2x1-x2的最大值为( )
| A. | $\frac{23}{12}π$ | B. | $\frac{35}{12}π$ | C. | $\frac{19}{6}π$ | D. | $\frac{59}{12}π$ |
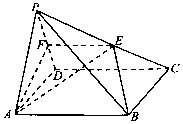 如图,在四棱锥P-ABCD中,底面ABCD是矩形,点E在棱PC上(异于点P,C),平面ABE与棱PD交于点F.
如图,在四棱锥P-ABCD中,底面ABCD是矩形,点E在棱PC上(异于点P,C),平面ABE与棱PD交于点F.