题目内容
13.已知△ABC中,$AC=2,A=\frac{2π}{3},\sqrt{3}cosC=3sinB$.(1)求AB;
(2)若D为BC边上一点,且△ACD的面积为$\frac{{3\sqrt{3}}}{4}$,求∠ADC的正弦值.
分析 (1)把B=$\frac{π}{3}-C$代入$\sqrt{3}$cosC=$\sqrt{3}$sinB化简即可得出C和B,于是△ABC是等腰三角形;
(2)根据面积公式计算CD,在△ACD中先利用余弦定理求出AD,在用正弦定理求出sin∠ADC.
解答 解析:(1)∵$A=\frac{2π}{3}$,∴$B=\frac{π}{3}-C$,
由$\sqrt{3}cosC=3sinB$得:$cosC=\sqrt{3}sin({\frac{π}{3}-C})$,
∴$cosC=\sqrt{3}({\frac{{\sqrt{3}}}{2}cosC-\frac{1}{2}sinC})=\frac{3}{2}cosC-\frac{{\sqrt{3}}}{2}sinC$,
∴$\frac{1}{2}cosC=\frac{{\sqrt{3}}}{2}sinC$,即$tanC=\frac{{\sqrt{3}}}{3}$.
∵C∈(0,π),∴$C=\frac{π}{6}$,
∴$B=\frac{π}{3}-C=\frac{π}{6}$,
∴AB=AC=2.
(2)∵S△ACD=$\frac{1}{2}•AC•CDsin\frac{π}{6}=\frac{{3\sqrt{3}}}{4}$,∴$CD=\frac{{3\sqrt{3}}}{2}$,
在△ACD中,由余弦定理得:$A{D^2}=A{C^2}+C{D^2}-2AC•CD•cosC=\frac{7}{4}$,∴$AD=\frac{{\sqrt{7}}}{2}$,
由正弦定理得,$\frac{AD}{sinC}=\frac{AC}{sin∠ADC}$,
∴$sin∠ADC=\frac{AC•sinC}{AD}=\frac{{2\sqrt{2}}}{7}$.
点评 本题考查了三角函数的恒等变换,正余弦定理解三角形,属于中档题.

 名校课堂系列答案
名校课堂系列答案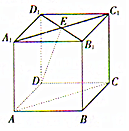 如图所示,在正方体AC1中,AB=2,A1C1∩B1D1=E,直线AC与直线DE所成的角为α,直线DE与平面BCC1B1所成的角为β,则cos(α-β)=( )
如图所示,在正方体AC1中,AB=2,A1C1∩B1D1=E,直线AC与直线DE所成的角为α,直线DE与平面BCC1B1所成的角为β,则cos(α-β)=( )| A. | $\frac{\sqrt{6}}{6}$ | B. | $\frac{\sqrt{3}}{3}$ | C. | $\frac{\sqrt{30}}{6}$ | D. | $\frac{\sqrt{6}}{3}$ |
| A. | (0,1) | B. | (0,1] | C. | (-1,1) | D. | (-1,0] |
| A. | p∨q | B. | (¬p)∨q | C. | (¬p)∧q | D. | (¬p)∧(¬q) |
| A. | $\frac{1}{2}-\frac{3}{2}i$ | B. | $\frac{1}{2}+\frac{3}{2}i$ | C. | 1+3i | D. | 1-3i |
| A. | N⊆M | B. | M⊆N | C. | M∩N=N | D. | M∩N={2} |
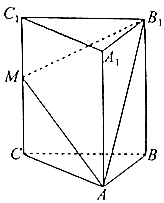 如图,在三棱柱ABC-A1B1C1中,CC1⊥平面ABC,M是CC1中点.
如图,在三棱柱ABC-A1B1C1中,CC1⊥平面ABC,M是CC1中点.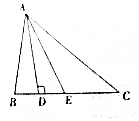 如图,在△ABC中,AD是BC上的高,AE平分∠BAC,∠B=75°,∠C=45°,求∠DAE与∠AEC的度数.
如图,在△ABC中,AD是BC上的高,AE平分∠BAC,∠B=75°,∠C=45°,求∠DAE与∠AEC的度数.