题目内容
如图,在五棱锥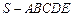 中,
中,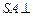 底面
底面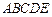 ,
,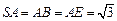 ,
,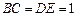 ,
,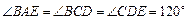 。
。
(1)证明: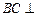 平面
平面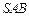 ;
;
(2)求二面角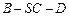 的余弦值。
的余弦值。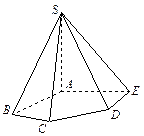
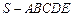 中,
中,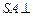 底面
底面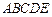 ,
,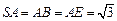 ,
,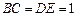 ,
,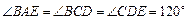 。
。(1)证明:
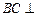 平面
平面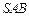 ;
;(2)求二面角
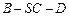 的余弦值。
的余弦值。
(1)见解析 (2) 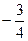
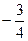
(1)证明:由题意,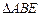 是等腰三角形,
是等腰三角形,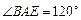 ,所以
,所以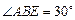 . 又
. 又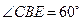 ,∴
,∴ 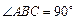 ,所以
,所以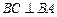 .∵
.∵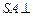 底面
底面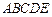 ,
,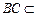 底面
底面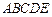 ,
,
∴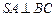 ,又
,又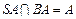 ,∴
,∴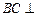 平面
平面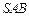 .…………………………………5分
.…………………………………5分
(2)解:易证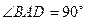 ,以
,以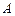 为原点,AB、AD、AS所在直线分别为
为原点,AB、AD、AS所在直线分别为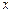 轴、
轴、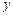 轴、
轴、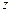 轴,建立空间直角坐标系(如图),
轴,建立空间直角坐标系(如图),
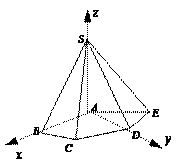
则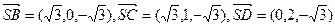 ,
,
设平面SBC的法向量为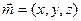 ,设平面SCD的法向量为
,设平面SCD的法向量为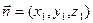
由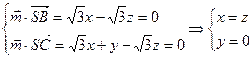 ,令
,令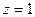 ,则
,则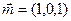 ,
,
同理可求,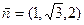 ∴
∴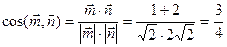 ,
,
∴二面角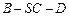 的余弦值为
的余弦值为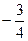 .………………13分
.………………13分
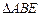 是等腰三角形,
是等腰三角形,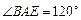 ,所以
,所以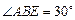 . 又
. 又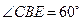 ,∴
,∴ 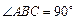 ,所以
,所以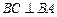 .∵
.∵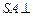 底面
底面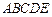 ,
,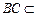 底面
底面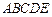 ,
,∴
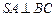 ,又
,又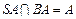 ,∴
,∴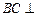 平面
平面 .…………………………………5分
.…………………………………5分(2)解:易证
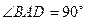 ,以
,以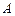 为原点,AB、AD、AS所在直线分别为
为原点,AB、AD、AS所在直线分别为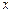 轴、
轴、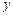 轴、
轴、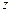 轴,建立空间直角坐标系(如图),
轴,建立空间直角坐标系(如图),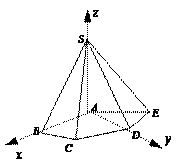
则
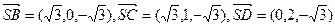 ,
,设平面SBC的法向量为
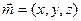 ,设平面SCD的法向量为
,设平面SCD的法向量为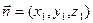
由
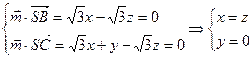 ,令
,令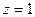 ,则
,则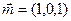 ,
,同理可求,
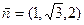 ∴
∴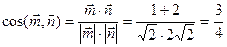 ,
,∴二面角
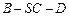 的余弦值为
的余弦值为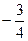 .………………13分
.………………13分
练习册系列答案
相关题目
 平面
平面 ,
,
 ,且
,且 ,(1)求证:BE//平面PDA;
,(1)求证:BE//平面PDA; 的中点,求证:
的中点,求证: 平面
平面 ;
; ,求平面PBE与平面ABCD所成的二面角的大小.
,求平面PBE与平面ABCD所成的二面角的大小.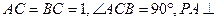 平面ABC,CE//PA,PA=2CE=2。
平面ABC,CE//PA,PA=2CE=2。 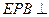 平面APB; (2)求二面角A—BE—P的正弦值。
平面APB; (2)求二面角A—BE—P的正弦值。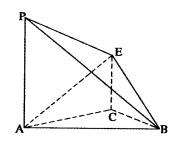
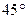 ,M为AB中点,N为SC中点.
,M为AB中点,N为SC中点.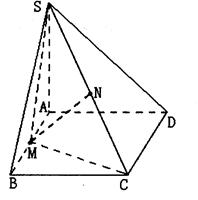
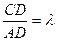 ,求实数
,求实数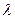 的值,使得直线SM与平面SCD所成角为
的值,使得直线SM与平面SCD所成角为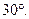
 平面
平面 =
= ,
, ,且
,且 ,二面角
,二面角 .
.  到平面
到平面 的大小为
的大小为 ,求
,求 的值.
的值.
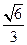
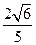
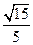
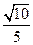
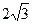 ,侧棱与底面所成的角为
,侧棱与底面所成的角为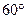 ,则该棱锥的体积为( )
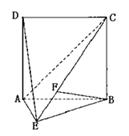
,则该棱锥的体积为( )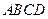 中,
中,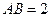 ,
,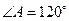 ,沿对角线
,沿对角线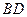 将
将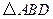 折起,使二面角
折起,使二面角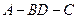 为
为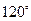 ,则点
,则点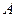 到
到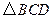 所在平面的距离等于 。
所在平面的距离等于 。