题目内容
已知坐标平面内⊙C:(x+1)2+y2=
,⊙D:(x-1)2+y2=
.动圆P与⊙C 外切,与⊙D内切.
(1)求动圆圆心P的轨迹C1的方程;
(2)若过D点的斜率为2的直线与曲线C1交于两点A、B,求AB的长;
(3)过D的动直线与曲线C1交于A、B两点,线段AB中点为M,求M的轨迹方程.
| 1 |
| 4 |
| 49 |
| 4 |
(1)求动圆圆心P的轨迹C1的方程;
(2)若过D点的斜率为2的直线与曲线C1交于两点A、B,求AB的长;
(3)过D的动直线与曲线C1交于A、B两点,线段AB中点为M,求M的轨迹方程.
考点:轨迹方程,与直线有关的动点轨迹方程
专题:圆锥曲线的定义、性质与方程
分析:(1)根据动圆P与⊙C 外切,与⊙D内切,由椭圆定义可知,点P的轨迹是以C(-1,0)、D(1,0)为焦点的椭圆;
(2)求出直线AB的方程与椭圆方程联立,利用弦长公式,可求AB的长;
(3)由点差法可得KOM•KAB=-
=-
,从而可求M的轨迹方程.
(2)求出直线AB的方程与椭圆方程联立,利用弦长公式,可求AB的长;
(3)由点差法可得KOM•KAB=-
| b2 |
| a2 |
| 3 |
| 4 |
解答:
解:(1)据题意,当令动圆半径为r时,有
,所以|PC|+|PD|=4
由椭圆定义可知,点P的轨迹是以C(-1,0)、D(1,0)为焦点的椭圆.
令椭圆方程为
+
=1,(a>b>0)
所以a=2,b2=22-1=3,所以P的轨迹方程为
+
=1.
(2)过D点斜率为2的直线方程为:y=2x-2.
由
,消y得到19x2-32x+4=0,
∴|AB|=
=
;
(3)由点差法可得KOM•KAB=-
=-
,
若令M坐标为(x,y),则有
•
=-
,
化简可得:3x2+4y2-3x=0.
|
由椭圆定义可知,点P的轨迹是以C(-1,0)、D(1,0)为焦点的椭圆.
令椭圆方程为
| x2 |
| a2 |
| x2 |
| b2 |
所以a=2,b2=22-1=3,所以P的轨迹方程为
| x2 |
| 4 |
| y2 |
| 3 |
(2)过D点斜率为2的直线方程为:y=2x-2.
由
|
∴|AB|=
| 1+22 |
| ||
| 19 |
| 60 |
| 19 |
(3)由点差法可得KOM•KAB=-
| b2 |
| a2 |
| 3 |
| 4 |
若令M坐标为(x,y),则有
| y |
| x |
| y |
| x-1 |
| 3 |
| 4 |
化简可得:3x2+4y2-3x=0.
点评:本题考查椭圆的定义与方程,考查直线与椭圆的位置关系,考查学生的计算能力,属于中档题.

练习册系列答案
相关题目
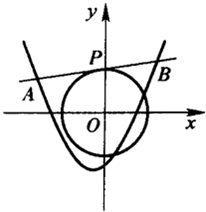 设点P(m,n)在圆x2+y2=2上,l是过点P的圆的切线,切线l与函数y=x2+x+k(k∈R)的图象交于AB两点,点O是坐标原点,且△OAB是以AB为底的等腰三角形;
设点P(m,n)在圆x2+y2=2上,l是过点P的圆的切线,切线l与函数y=x2+x+k(k∈R)的图象交于AB两点,点O是坐标原点,且△OAB是以AB为底的等腰三角形;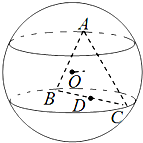 正三角形ABC的三个顶点都在半径为2的球面上,球心O到平面ABC的距离为1,点D是线段BC的中点,过D作球O的截面,则截面面积的最小值为
正三角形ABC的三个顶点都在半径为2的球面上,球心O到平面ABC的距离为1,点D是线段BC的中点,过D作球O的截面,则截面面积的最小值为