题目内容

2．下列函数中既是奇函数，又在区间（0，+∞）上是单调递减的函数为（　　）
A．y=$\sqrt{x}$B．y=-x3C．y=${log_{\frac{1}{2}}}$xD．y=x+$\frac{1}{x}$

分析 根据函数的奇偶性和单调性，对选项中的函数进行分析判断即可．

解答 解：对于A，y=$\sqrt{x}$（x≥0）是非奇非偶的函数，不满足条件；
对于B，y=-x3，是定义域R上的奇函数，且在区间（0，+∞）上是单调减函数，满足条件；
对于C，y=${log}_{\frac{1}{2}}$x，定义域是（0，+∞），是非奇非偶的函数，不满足条件；
对于D，y=x+$\frac{1}{x}$，是定义域（-∞，0）∪（0，+∞）上的奇函数，
但在区间（0，+∞）上不是单调减函数，也不满足题意．
故选：B．

点评 本题主要考查了函数奇偶性和单调性的判断问题，是基础题目．

练习册系列答案
相关题目
12．若直线y=kx+2是函数f（x）=x3-x2-3x-1的图象的一条切线，则k=（　　）
A．1B．-1C．2D．-2
13．一名顾客计划到某商场购物，他有三张商场的优惠劵，商场规定每购买一件商品只能使用一张优惠券．根据购买商品的标价，三张优惠券的优惠方式不同，具体如下：
优惠劵A：若商品标价超过50元，则付款时减免标价的10%；
优惠劵B：若商品标价超过100元，则付款时减免20元；
优惠劵C：若商品标价超过100元，则付款时减免超过100元部分的18%．
某顾客想购买一件标价为150元的商品，若想减免钱款最多，则应该使用B优惠劵（填A，B，C）；若顾客想使用优惠券C，并希望比优惠券A和B减免的钱款都多，则他购买的商品的标价应高于225元．
10．已知F1、F2分别是双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1（a＞0，b＞0）的左右焦点，若在双曲线的右支上存在一点M，使得（$\overrightarrow{OM}$+$\overrightarrow{O{F}_{2}}$）•$\overrightarrow{{F}_{2}M}$=0（其中O为坐标原点），且|$\overrightarrow{M{F}_{1}}$|=$\sqrt{3}$|$\overrightarrow{M{F}_{2}}$|，则双曲线离心率为$\sqrt{3}$+1．
17．函数f（x）=$\frac{{\sqrt{4-{x^2}}}}{{{{log}_2}x-1}}$的定义域为（0，2）．
7．已知数列{an}的前n项和为Sn，且Sn=$\frac{1}{2}$（3an-1）．数列{bn}为等差数列，b1=a1，b2=a3．
（Ⅰ）求数列{an}，{bn}的通项公式；
（Ⅱ）设cn=$\frac{{4（{n^2}+n+1）}}{{b_{n+1}^2-1}}$，求数列{cn}的前n项和Tn．
14．已知复数z满足z=$\frac{5}{2-i}$，则|z|=（　　）
A．2B．$\sqrt{5}$C．3D．5
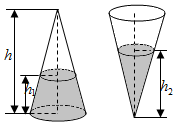11．如图，圆锥形容器的高为h，圆锥内水面的高为h1，且$\frac{h_1}{h}$=$\frac{1}{3}$，若将圆锥倒置，水面高为h2，则$\frac{h_2}{h}$等于$\frac{\root{3}{19}}{3}$．
12．已知椭圆C：$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）的两个焦点分别为F1（-$\sqrt{2}$，0），F2（$\sqrt{2}$，0），以椭圆短轴为直径的圆经过点M（1，0）．
（1）求椭圆C的方程；
（2）过点M的直线l与椭圆C相交于A、B两点，设点N（3，2），记直线AN，BN的斜率分别为k1，k2，问：k1+k2是否为定值？并证明你的结论．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网