题目内容
13.一名顾客计划到某商场购物,他有三张商场的优惠劵,商场规定每购买一件商品只能使用一张优惠券.根据购买商品的标价,三张优惠券的优惠方式不同,具体如下:优惠劵A:若商品标价超过50元,则付款时减免标价的10%;
优惠劵B:若商品标价超过100元,则付款时减免20元;
优惠劵C:若商品标价超过100元,则付款时减免超过100元部分的18%.
某顾客想购买一件标价为150元的商品,若想减免钱款最多,则应该使用B优惠劵(填A,B,C);若顾客想使用优惠券C,并希望比优惠券A和B减免的钱款都多,则他购买的商品的标价应高于225元.
分析 根据条件,分别求出减免钱款,可得结论;利用顾客想使用优惠券C,并希望比优惠券A和B减免的钱款都多,建立不等式,即可求出他购买的商品的标价的最低价.
解答 解:标价为150元的商品,使用优惠劵A,付款时减免15元;使用优惠劵B,付款时减免20元;使用优惠劵C,付款时减免9元,故想减免钱款最多,则应该使用优惠劵B.
设标价为x元,则(x-100)×18%>x×10%且(x-100)×18%>20,∴x>225,即他购买的商品的标价应高于225元.
故答案为:B;225.
点评 本题考查利用数学知识解决实际问题,考查学生分析解决问题的能力,比较基础.

练习册系列答案
 寒假乐园北京教育出版社系列答案
寒假乐园北京教育出版社系列答案
相关题目
1.若实数a,b,c,d满足a2-lna=b,d=c-2,则(a-c)2+(b-d)2的最小值为( )
| A. | 1 | B. | $\sqrt{2}$ | C. | 2 | D. | 4 |
8.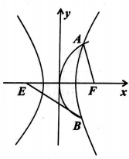 已知E,F为双曲线C:$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(0<a<b)的左右焦点,抛物线y2=2px(p>0)与双曲线有公共的焦点F,且与双曲线交于A,B不同两地两点,若|AF|=$\frac{4}{5}$|BE|,则双曲线的离心率为( )
已知E,F为双曲线C:$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(0<a<b)的左右焦点,抛物线y2=2px(p>0)与双曲线有公共的焦点F,且与双曲线交于A,B不同两地两点,若|AF|=$\frac{4}{5}$|BE|,则双曲线的离心率为( )
 已知E,F为双曲线C:$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(0<a<b)的左右焦点,抛物线y2=2px(p>0)与双曲线有公共的焦点F,且与双曲线交于A,B不同两地两点,若|AF|=$\frac{4}{5}$|BE|,则双曲线的离心率为( )
已知E,F为双曲线C:$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(0<a<b)的左右焦点,抛物线y2=2px(p>0)与双曲线有公共的焦点F,且与双曲线交于A,B不同两地两点,若|AF|=$\frac{4}{5}$|BE|,则双曲线的离心率为( )| A. | 4-$\sqrt{7}$ | B. | 4-$\sqrt{3}$ | C. | 4+$\sqrt{3}$ | D. | 4+$\sqrt{7}$ |
18.设x∈R,且x≠0,“($\frac{1}{2}$)x>1”是“$\frac{1}{x}$<1”的( )
| A. | 充分而不必要条件 | B. | 必要而不充分条件 | ||
| C. | 充分必要条件 | D. | 既不充分也不必要条件 |
5.已知{an}为等差数列,3a4+a8=36,则{an}的前9项和S9=( )
| A. | 9 | B. | 17 | C. | 36 | D. | 81 |
2.下列函数中既是奇函数,又在区间(0,+∞)上是单调递减的函数为( )
| A. | y=$\sqrt{x}$ | B. | y=-x3 | C. | y=${log_{\frac{1}{2}}}$x | D. | y=x+$\frac{1}{x}$ |
 对某高三学生在连续9次数学测试中的成绩(单位:分)进行统计得到如下折线图.下面关于这位同学的数学成绩的分析中,正确的共有( )个
对某高三学生在连续9次数学测试中的成绩(单位:分)进行统计得到如下折线图.下面关于这位同学的数学成绩的分析中,正确的共有( )个