题目内容
10.已知F1、F2分别是双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的左右焦点,若在双曲线的右支上存在一点M,使得($\overrightarrow{OM}$+$\overrightarrow{O{F}_{2}}$)•$\overrightarrow{{F}_{2}M}$=0(其中O为坐标原点),且|$\overrightarrow{M{F}_{1}}$|=$\sqrt{3}$|$\overrightarrow{M{F}_{2}}$|,则双曲线离心率为$\sqrt{3}$+1.分析 根据向量关系求出F1M⊥MF2,结合双曲线的定义以及直角三角形的边角关系建立方程关系进行求解即可.
解答 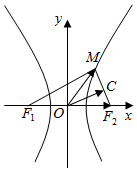 解:设C是MF2的中点,
解:设C是MF2的中点,
∵($\overrightarrow{OM}$+$\overrightarrow{O{F}_{2}}$)•$\overrightarrow{{F}_{2}M}$=0
∴2$\overrightarrow{OC}$•$\overrightarrow{{F}_{2}M}$=0
即OC⊥MF2,
即OM=OF2
∵OC∥F1M,
∴F1M⊥MF2,
∵|$\overrightarrow{M{F}_{1}}$|=$\sqrt{3}$|$\overrightarrow{M{F}_{2}}$|,
∴|$\overrightarrow{M{F}_{1}}$|-|$\overrightarrow{M{F}_{2}}$|=$\sqrt{3}$|$\overrightarrow{M{F}_{2}}$|-|$\overrightarrow{M{F}_{2}}$|=2a
则|$\overrightarrow{M{F}_{2}}$|=$\frac{2a}{\sqrt{3}-1}$=($\sqrt{3}$+1)a,
|$\overrightarrow{M{F}_{1}}$|=$\sqrt{3}$|$\overrightarrow{M{F}_{2}}$|=$\sqrt{3}$($\sqrt{3}$+1)a,
∵|$\overrightarrow{M{F}_{1}}$|2+|$\overrightarrow{M{F}_{2}}$|2=4c2,
∴4($\sqrt{3}$+1)2a2=4c2,
即($\sqrt{3}$+1)2a2=c2,
即($\sqrt{3}$+1)a=c,
则离心率e=$\frac{c}{a}$=$\sqrt{3}$+1,
故答案为:$\sqrt{3}$+1
点评 本题主要考查双曲线离心率的计算,根据向量关系判断F1M⊥MF2,是解决本题的关键.综合性较强,有一定的难度.

| A. | $\frac{π}{3}$<α≤$\frac{5π}{6}$ | B. | $\frac{π}{3}$<α<π | C. | $\frac{π}{3}$≤α<π | D. | $\frac{π}{3}$<α≤$\frac{2π}{3}$ |
| A. | 1 | B. | $\sqrt{2}$ | C. | 2 | D. | 4 |
| A. | 充分而不必要条件 | B. | 必要而不充分条件 | ||
| C. | 充分必要条件 | D. | 既不充分也不必要条件 |
| A. | 9 | B. | 17 | C. | 36 | D. | 81 |
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
| A. | y=$\sqrt{x}$ | B. | y=-x3 | C. | y=${log_{\frac{1}{2}}}$x | D. | y=x+$\frac{1}{x}$ |