题目内容
17．函数f（x）=$\frac{{\sqrt{4-{x^2}}}}{{{{log}_2}x-1}}$的定义域为（0，2）．分析 根据函数成立的条件即可求函数的定义域．
解答 解：要使函数有意义，则$\left\{\begin{array}{l}{4-{x}^{2}≥0}\\{lo{g}_{2}x-1≠0}\\{x＞0}\end{array}\right.$．
即$\left\{\begin{array}{l}{-2≤x≤2}\\{x≠2}\\{x＞0}\end{array}\right.$，即0＜x＜2，
即函数的定义域为（0，2），
故答案为：（0，2）．
点评 本题主要考查函数的定义域的求解，要求熟练掌握常见函数成立的条件．比较基础．
练习册系列答案
英语小英雄天天默写系列答案
暑假作业安徽少年儿童出版社系列答案
相关题目
7．已知函数f（x）=x2-ax的图象在点A（1，f（1））处的切线l与直线x+3y-1=0垂直，记数列$\{\frac{1}{f（n）}\}$的前n项和为Sn，则S2016的值为（ ）
| A． | $\frac{2015}{2016}$ | B． | $\frac{2016}{2017}$ | C． | $\frac{2014}{2015}$ | D． | $\frac{2017}{2018}$ |
8．
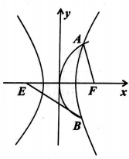已知E，F为双曲线C：$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1（0＜a＜b）的左右焦点，抛物线y2=2px（p＞0）与双曲线有公共的焦点F，且与双曲线交于A，B不同两地两点，若|AF|=$\frac{4}{5}$|BE|，则双曲线的离心率为（ ）
已知E，F为双曲线C：$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1（0＜a＜b）的左右焦点，抛物线y2=2px（p＞0）与双曲线有公共的焦点F，且与双曲线交于A，B不同两地两点，若|AF|=$\frac{4}{5}$|BE|，则双曲线的离心率为（ ）| A． | 4-$\sqrt{7}$ | B． | 4-$\sqrt{3}$ | C． | 4+$\sqrt{3}$ | D． | 4+$\sqrt{7}$ |
5．已知{an}为等差数列，3a4+a8=36，则{an}的前9项和S9=（ ）
| A． | 9 | B． | 17 | C． | 36 | D． | 81 |
2．下列函数中既是奇函数，又在区间（0，+∞）上是单调递减的函数为（ ）
| A． | y=$\sqrt{x}$ | B． | y=-x3 | C． | y=${log_{\frac{1}{2}}}$x | D． | y=x+$\frac{1}{x}$ |
6．在△ABC中，“A=B”是“sinAcosA=sinBcosB”的（ ）
| A． | 充分不必要条件 | B． | 必要不充分条件 | ||
| C． | 充要条件 | D． | 既不充分也不必要条件 |
7．设数列{an}的前n项和为Sn，且a1=$\frac{1}{2}$，{Sn+nan}为常数列，则an=（ ）
| A． | $\frac{1}{n（n+1）}$ | B． | $\frac{1}{{2}^{n}}$ | C． | $\frac{3}{（n+1）（n+2）}$ | D． | $\frac{5-2n}{6}$ |