题目内容
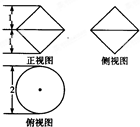某几何体的三视图如图所示，则该几何体的体积为（ ）A、
| ||
B、2
| ||
C、
| ||
D、
|
考点：由三视图求面积、体积
专题：计算题,空间位置关系与距离
分析：由题意，几何体为共底面的两个圆锥，两个圆锥的底面半径为1，高为1，可得几何体的体积．
解答：
解：由题意，几何体为共底面的两个圆锥，两个圆锥的底面半径为1，高为1，
故几何体的体积为2×
π×12×1=
，
故选：D．
故几何体的体积为2×
| 1 |
| 3 |
| 2π |
| 3 |
故选：D．
点评：本题考查了几何体的三视图及直观图的画法，三视图与直观图的关系，圆锥的体积计算公式，空间想象能力，比较基础．
练习册系列答案
提分百分百检测卷系列答案
相关题目
已知等比数列{an}的前n项和为Sn，a1+a3+a5-（a2+a4）=8，a12+a32+a52+（a22+a42）=12，则S5=（ ）
A、-
| ||
B、
| ||
C、
| ||
D、-
|
如图，在圆C：x2+y2=10内随机撒一粒豆子，则豆子落在阴影部分的概率是（ ）
A、1-
| ||
B、
| ||
C、
| ||
D、
|
已知函数f（x）=
若f（f（0））≥a2-1，则实数a的取值范围为（ ）
|
| A、[3，4] |
| B、[2，3] |
| C、[1，2] |
| D、[-1，2] |