题目内容
若方程2x2-(
)x+m=0的两根为sinα,cosα,α∈(0,π).
(1)求m的值;
(2)求
-
的值.
| 3-1 |
(1)求m的值;
(2)求
| sinα | ||
1+
|
| cosα |
| 1+tanα |
考点:三角函数的化简求值
专题:计算题,三角函数的求值
分析:(1)利用根与系数的关系列出关系式,变形即可求出m的值;
(2)由同角三角函数基本关系化简所求后代入(1)的结论即可求值.
(2)由同角三角函数基本关系化简所求后代入(1)的结论即可求值.
解答:
解:(1)由根与系数的关系可知,sinθ+cosθ=
①,sinθ•cosθ=
②,
将①式平方得1+2sinθ•cosθ=
,即sinθ•cosθ=-
,
代入②得m=-
;
(2)∵(sinα-cosα)2=1-2sinαcosα=1-2×(-
)=
.
-
=
-
=sinα-cosα=+
.
| ||
| 2 |
| m |
| 2 |
将①式平方得1+2sinθ•cosθ=
| 1 |
| 2 |
| 1 |
| 4 |
代入②得m=-
| 1 |
| 2 |
(2)∵(sinα-cosα)2=1-2sinαcosα=1-2×(-
| 1 |
| 4 |
| 3 |
| 2 |
| sinα | ||
1+
|
| cosα |
| 1+tanα |
| sin2α |
| sinα+cosα |
| cos2α |
| sinα+cosα |
| ||
| 2 |
点评:此题考查了同角三角函数基本关系的运用,熟练掌握基本关系是解本题的关键,属于基础题.

练习册系列答案
 小学期末冲刺100分系列答案
小学期末冲刺100分系列答案 期末复习检测系列答案
期末复习检测系列答案 超能学典单元期中期末专题冲刺100分系列答案
超能学典单元期中期末专题冲刺100分系列答案 黄冈360度定制密卷系列答案
黄冈360度定制密卷系列答案
相关题目
程序框图如图所示:如果程序运行的结果S=1320,那么判断框中应填入( )


| A、K<10 | B、K≤10 |
| C、K<9 | D、K≤11 |
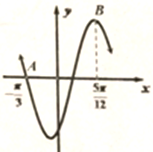 函数f(x)=2sin(ωx+φ)(ω>0,-
函数f(x)=2sin(ωx+φ)(ω>0,-| π |
| 2 |
| π |
| 2 |
A、2,-
| ||
B、2,-
| ||
C、4,-
| ||
D、4,
|
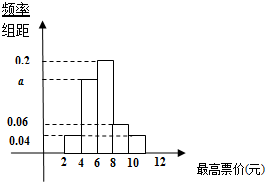 2014年5月,北京市提出地铁分段计价的相关意见,针对“你能接受的最高票价是多少?”这个问题,在某地铁站口随机对50人进行调查,调查数据的频率分布直方图及被调查者中35岁以下的人数与统计结果如下:
2014年5月,北京市提出地铁分段计价的相关意见,针对“你能接受的最高票价是多少?”这个问题,在某地铁站口随机对50人进行调查,调查数据的频率分布直方图及被调查者中35岁以下的人数与统计结果如下:



